Question

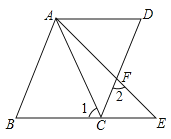
【题目】如图，有一组平行线l1∥l2∥l3∥l4，正方形ABCD的四个顶点A，B，C，D分别在l1，l2，l3，l4上，过点D作DE⊥l1于点E，已知相邻两条平行线之间的距离为1，求AE及正方形ABCD的边长．

Answer 1

【答案】AE＝1，AD＝.

【解析】

过点B作BF⊥l1，垂足为点F，由正方形的性质可得出∠BAD＝90°，AB＝AD，再由垂直可得出∠BFA＝∠AED＝90°，通过角的计算得出∠EAD＝∠FBA，由此即可证出△FAB≌△EDA(AAS)，根据全等三角形的性质以及勾股定理即可求出AE、AD的长度．

过点B作BF⊥⊥l1，垂足为点F，如图所示．

∵四边形ABCD为正方形，

∴∠BAD＝90°，AB＝AD，

∵BF⊥l1，DE⊥l1，

∴∠FAB＋∠EAD＝90°，∠FAB＋∠FBA＝90°，∠BFA＝∠AED＝90°，

∴∠EAD＝∠FBA，

在△FAB和△EDA中，

，

∴△FAB≌△EDA(AAS)，

∴AE＝BF＝1，

∵ED＝2，

∴AD＝＝.