搜索
【题目】如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=5 
cm，且tan∠EFC= 
，则矩形ABCD的周长是 ． 
参考答案：
【答案】36cm
【解析】解：设CE=3k，则CF=4k，由勾股定理得EF=DE=5k，
∴DC=AB=8k，
∵∠AFB+∠BAF=90°，∠AFB+∠EFC=90°，
∴∠BAF=∠EFC，
∴tan∠BAF=tan∠EFC= 
，
∴BF=6k，AF=BC=AD=10k，
在Rt△AFE中由勾股定理得AE= 
= 
=5 
，
解得：k=1，
故矩形ABCD的周长=2（AB+BC）=2（8k+10k）=36cm．
【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE＝BF，连接DE，过点E作EG⊥DE，使EG＝DE，连接FG，FC.
(1)请判断：FG与CE的数量关系是__________，位置关系是__________；
(2)如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，(1)中结论是否仍然成立？请出判断判断并给予证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A，E，F，C在一条直线上，AE＝CF，过E，F分别作DE⊥AC，BF⊥AC，若AB＝CD，试证明BD平分EF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有一组平行线l1∥l2∥l3∥l4，正方形ABCD的四个顶点A，B，C，D分别在l1，l2，l3，l4上，过点D作DE⊥l1于点E，已知相邻两条平行线之间的距离为1，求AE及正方形ABCD的边长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCF中，∠ACB＝90°，点E是AB边的中点，点F恰是点E关于AC所在直线的对称点．
(1)证明：四边形CFAE为菱形；
(2)连接EF交AC于点O，若BC＝10，求线段OF的长．
-
科目： 来源： 题型：
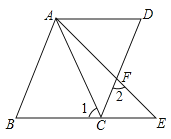
查看答案和解析>>【题目】已知AD∥BE，∠B=∠D．
（1）求证：AB∥CD；
（2）若∠1=∠2=60°，∠BAC=3∠EAC，求∠DCE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下表是根据对初一（1）班的50名同学平时最爱吃的食物的种类进行的问卷调查绘制成的统计表，请填满缺少的项并回答后面的问题．
肉类
蔬菜类
瓜果类
水产类
男生
22
1
2
女生
4
5
3
频率
64%
14%
12%
（1）选择适当的统计图表示男生平时最爱吃的食物的种类情况；
（2）就给出的初一（1）班的同学平时最爱吃的食物的种类情况，请你结合自己的年龄特点简略谈谈自己的看法．
相关试题
