搜索
【题目】对于二次函数 y ax2 2a 1x a 1a 0，有下列结论：①其图象与 x 轴一定相交；②若 a 0 ， 函数在 x 1 时，y 随 x 的增大而减小；③无论 a 取何值，抛物线的顶点始终在同一条直线上；④无论 a 取何值，函数图象都经过同一个点．其中所有正确的结论是:（ ）
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
参考答案：
【答案】B
【解析】试题解析：令y=0,则
解得
所以,函数图象与x轴的交点为
故①④正确；
当a<0时, 
所以，函数在x>1时，y先随x的增大而增大，然后再减小，故②错误；
即无论a取何值,抛物线的顶点始终在直线
上，故③正确；
综上所述，正确的结论是①③④。
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小明遇到这样一个问题：如图1，在△ABC中，DE∥BC分别交AB于D，交AC于E．已知CD⊥BE，CD=3，BE=4，求BC+DE的值．
小明发现，过点E作EF∥DC，交BC延长线于点F，构造△BEF，经过推理和计算能够使问题得到解决（如图2）．
（1）请按照上述思路完成小明遇到的这个问题
（2）参考小明思考问题的方法，解决问题：
如图3，已知ABCD和矩形ABEF，AC与DF交于点G，AC=BF=DF，求∠DGC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（提出问题）（1）如图1，已知AB∥CD，证明：∠1+∠EPF+∠2＝360°；
（类比探究）（2）如图2，已知AB∥CD，设从E点出发的（n﹣1）条折线形成的n个角分别为∠1，∠2……∠n，探索∠1+∠2+∠3+……+∠n的度数可能在1700°至2000°之间吗？若有可能请求出n的值，若不可能请说明理由．
（拓展延伸）（3）如图3，已知AB∥CD，∠AE1E2的角平分线E1O与∠CEnEn﹣1的角平分线EnO交于点O，若∠E1OEn＝m°．求∠2+∠3+∠4+…+∠（n﹣1）的度数．（用含m、n的代数式表示）
-
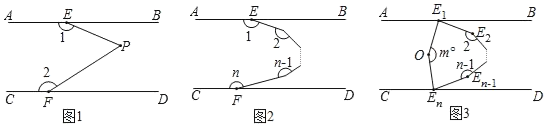
科目： 来源： 题型：
查看答案和解析>>【题目】某市为创建生态文明建设城市，对公路旁的绿化带进行全面改造．现有甲、乙两个工程队，甲队单独完成这项工程，刚好如期完成，每施工一天，需付工程款1.5万元；乙工程队单独完成这项工程要比规定工期多用a天，乙工程队每施工一天需付工程款1万元．若先由甲、乙两队一起合作b天，剩下的工程由乙队单独做，也正好如期完工
（1）当a＝6，b＝4时，求工程预定工期的天数．
（2）若a﹣b＝2．a是偶数
①求甲队、乙队单独完成工期的天数（用含a的代数式表示）
②工程领导小组有三种施工方案：
方案一：甲队单独完成这项工程；
方案二：乙队单独完成这项工程；
方案三：先由甲、乙两队一起合作b天，剩下的工程由乙队单独做．
为了节省工程款，同时又能如期完工，请你选择一种方案，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角三角形
中，
，
平分
交
于点
，
平分
交
于点
，、相交于点
，过点作
，过点
作
交
于点
.下列结论：①
；②
；③平分
；④
.其中正确的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】最近流感高发期，在预防流感期间学校坚持天天消毒，下图是某次消毒时教室内空气中消毒液浓度 y（单位：毫克/立方米）随时间 x（单位：分钟）的变化情况图．从开始喷药到喷药结束的 10 分钟内（包括第十分钟），y 是 x 的二次函数；喷药结束后（从第十分钟开始），y 是 x 的反比例函数．
（1）如果点 A 是图中二次函数的顶点，求二次函数和反比例函数的解析式 （要写出自变量取值范围）；
（2）已知空气中消毒液浓度 y 不少于 15 毫克/立方米且持续时间不少于 8 分钟才能有效消毒，通过计算，请你回答这次消毒是否有效？
-
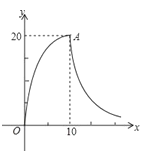
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB 是⊙O 的直径，CD 与⊙O 相切于点 C，与 AB 的延长线交于点 D，DE⊥AD 且与AC 的延长线交于点 E．
（1）求证：DC=DE；
（2）若 AD=2ED，AB=3，求BD的长．
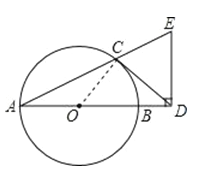
相关试题
