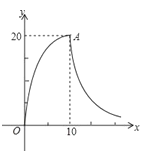
【题目】最近流感高发期,在预防流感期间学校坚持天天消毒,下图是某次消毒时教室内空气中消毒液浓度 y(单位:毫克/立方米)随时间 x(单位:分钟)的变化情况图.从开始喷药到喷药结束的 10 分钟内(包括第十分钟),y 是 x 的二次函数;喷药结束后(从第十分钟开始),y 是 x 的反比例函数.
(1)如果点 A 是图中二次函数的顶点,求二次函数和反比例函数的解析式 (要写出自变量取值范围);
(2)已知空气中消毒液浓度 y 不少于 15 毫克/立方米且持续时间不少于 8 分钟才能有效消毒,通过计算,请你回答这次消毒是否有效?
参考答案:
【答案】(1)v=-![]() ( x-10)2+20(0≤x≤10);(2) y=
( x-10)2+20(0≤x≤10);(2) y=![]() ;(3) 这次消毒有效.
;(3) 这次消毒有效.
【解析】试题分析:(1)由![]() 为抛物线顶点,设二次函数的顶点式,将
为抛物线顶点,设二次函数的顶点式,将![]() 代入可求二次函数解析式,再根据图象求自变量取值范围,设反比例函数关系式为
代入可求二次函数解析式,再根据图象求自变量取值范围,设反比例函数关系式为![]() ,将
,将![]() 点坐标代入求
点坐标代入求![]() 的值即可,再根据图形求自变量取值范围;
的值即可,再根据图形求自变量取值范围;
(2)将![]() 分别代入二次函数、反比例函数解析式求
分别代入二次函数、反比例函数解析式求![]() ,再把所求的两个
,再把所求的两个![]() 值作差,进行判断.
值作差,进行判断.
试题解析:(1)依题意可知,A(10,20)为抛物线顶点,设二次函数解析式为![]()
把O(0,0)代入,得100a+20=0, ![]() 所以,二次函数解析式为
所以,二次函数解析式为![]()
设反比例函数关系式为![]() ,将A点坐标代入,得k=xy=200,
,将A点坐标代入,得k=xy=200,
所以,反比例函数关系式为![]()
(2)把y=15代入![]() 中,得
中,得![]()
解得x=5或x=15(舍去),
把y=15代入![]() 中,得
中,得![]()
而![]()
所以,这次消毒有效.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为创建生态文明建设城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,甲队单独完成这项工程,刚好如期完成,每施工一天,需付工程款1.5万元;乙工程队单独完成这项工程要比规定工期多用a天,乙工程队每施工一天需付工程款1万元.若先由甲、乙两队一起合作b天,剩下的工程由乙队单独做,也正好如期完工
(1)当a=6,b=4时,求工程预定工期的天数.
(2)若a﹣b=2.a是偶数
①求甲队、乙队单独完成工期的天数(用含a的代数式表示)
②工程领导小组有三种施工方案:
方案一:甲队单独完成这项工程;
方案二:乙队单独完成这项工程;
方案三:先由甲、乙两队一起合作b天,剩下的工程由乙队单独做.
为了节省工程款,同时又能如期完工,请你选择一种方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数 y ax2 2a 1x a 1a 0,有下列结论:①其图象与 x 轴一定相交;②若 a 0 , 函数在 x 1 时,y 随 x 的增大而减小;③无论 a 取何值,抛物线的顶点始终在同一条直线上;④无论 a 取何值,函数图象都经过同一个点.其中所有正确的结论是:( )
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形
 中,
中, ,
, 平分
平分 交
交 于点
于点 ,
, 平分
平分 交
交 于点
于点 ,
, 、
、 相交于点
相交于点 ,过点
,过点 作
作 ,过点
,过点 作
作 交
交 于点
于点 .下列结论:①
.下列结论:① ;②
;② ;③
;③ 平分
平分 ;④
;④ .其中正确的个数是( )
.其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
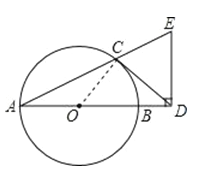
查看答案和解析>>【题目】如图,AB 是⊙O 的直径,CD 与⊙O 相切于点 C,与 AB 的延长线交于点 D,DE⊥AD 且与AC 的延长线交于点 E.
(1)求证:DC=DE;
(2)若 AD=2ED,AB=3,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乌鲁木齐周边多地盛产草莓,今年某水果销售店在草莓销售旺季,以15元/kg 的成本价进50kg有机草莓,销售人员销售发现草莓损坏率为25%;
(1)对于水果店来说完好的草莓实际成本价是多少元/kg?
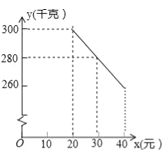
(2)按照这个实际成本设计销售单价,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象,设该水果销售店试销草莓获得的利润为W元,求W的最大值.
相关试题

