搜索
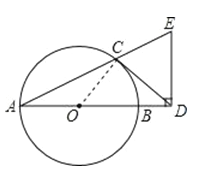
【题目】如图，AB 是⊙O 的直径，CD 与⊙O 相切于点 C，与 AB 的延长线交于点 D，DE⊥AD 且与AC 的延长线交于点 E．
（1）求证：DC=DE；
（2）若 AD=2ED，AB=3，求BD的长．
参考答案：
【答案】（1）证明见解析.（2）1.
【解析】试题分析：（1）利用切线的性质结合等腰三角形的性质得出
进而得出答案；
（2）设
则
利用勾股定理得出BD的长．
试题解析：(1)证明：连接OC，
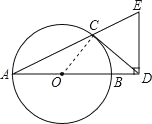
∵CD是
的切线，
又
∵OC=OA，∴∠ACO=∠EAD，
故∠DCE=∠E，
∴DC=DE，
(2)设BD=x，则AD=AB+BD=3+x，OD=OB+BD=1.5+x，
在
中，
∵
，
由(1)知, 
在
中，
则
解得： 
(舍去), 
故BD=1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数 y ax2 2a 1x a 1a 0，有下列结论：①其图象与 x 轴一定相交；②若 a 0 ， 函数在 x 1 时，y 随 x 的增大而减小；③无论 a 取何值，抛物线的顶点始终在同一条直线上；④无论 a 取何值，函数图象都经过同一个点．其中所有正确的结论是:（ ）
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角三角形
中，
，
平分
交
于点
，
平分
交
于点
，、相交于点
，过点作
，过点
作
交
于点
.下列结论：①
；②
；③平分
；④
.其中正确的个数是（ ）
A. 1个B. 2个C. 3个D. 4个
-
科目： 来源： 题型：
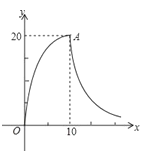
查看答案和解析>>【题目】最近流感高发期，在预防流感期间学校坚持天天消毒，下图是某次消毒时教室内空气中消毒液浓度 y（单位：毫克/立方米）随时间 x（单位：分钟）的变化情况图．从开始喷药到喷药结束的 10 分钟内（包括第十分钟），y 是 x 的二次函数；喷药结束后（从第十分钟开始），y 是 x 的反比例函数．
（1）如果点 A 是图中二次函数的顶点，求二次函数和反比例函数的解析式 （要写出自变量取值范围）；
（2）已知空气中消毒液浓度 y 不少于 15 毫克/立方米且持续时间不少于 8 分钟才能有效消毒，通过计算，请你回答这次消毒是否有效？
-
科目： 来源： 题型：
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理，分成5个小组（x表示成绩，单位：米）．A组：5.25≤x＜6.25；B组：6.25≤x＜7.25；C组：7.25≤x＜8.25；D组：8.25≤x＜9.25；E组：9.25≤x＜10.25，并绘制出扇形统计图和频数分布直方图（不完整）．规定x≥6.25为合格，x≥9.25为优秀．
（1）这部分男生有多少人？其中成绩合格的有多少人？
（2）这部分男生成绩的中位数落在哪一组？扇形统计图中D组对应的圆心角是多少度？
（3）要从成绩优秀的学生中，随机选出2人介绍经验，已知甲、乙两位同学的成绩均为优秀，求他俩至少有1人被选中的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】乌鲁木齐周边多地盛产草莓，今年某水果销售店在草莓销售旺季，以15元/kg 的成本价进50kg有机草莓，销售人员销售发现草莓损坏率为25%；
（1）对于水果店来说完好的草莓实际成本价是多少元/kg?
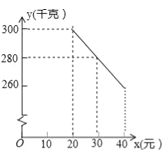
（2）按照这个实际成本设计销售单价，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量y（千克）与销售单价x（元）符合一次函数关系，如图是y与x的函数关系图象，设该水果销售店试销草莓获得的利润为W元，求W的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形
与
不平行，
．
为四边形
的对角线，
分别是
的中点下列结论：①
；②四边形
是矩形；③
平分
④
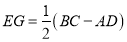；⑤四边形是菱形．其中正确的个数是 （ ）
A.
个B.
个C.
个D.
个
相关试题
