【题目】如图,在ABCD中,AD>AB,AM、BN、CP、DQ为四个内角的角平分线,P、为AD边上两点,其中AM与DQ相交于E,BN与CP相交于F,AM与BN相交于G,CP与DQ相交于H.
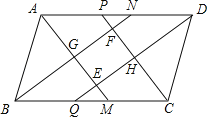
(1)求证:四边形EHFG是矩形.
(2)ABCD满足 时,四边形EHFG为正方形;ABCD满足 时,F点落在AD边上.(与点P、点N重合)
(3)探究矩形EHFG的对角线长度与ABCD的边长之间的数量关系,并证明.
参考答案:
【答案】(1)见解析; (2)∠BAD=90°,且BC=2AB ;BC=2AB;(3)GH=BC﹣AB;证明见解析.
【解析】
(1)根据平行线的性质及角平分线的定义证明四边形EHFG有三个角是直角即可;
(2)由(1)可得,四边形EHFG是矩形,若四边形EHFG为正方形,则有一组临边相等即可;若F点落在AD边上.(与点P、点N重合),则可得由(1)得:AF=AB,DF=CD,AG⊥BN,利用平行四边形的性质等量代换即可得到AB与BC的关系.
(3)连接EF、GH,由(1)(2)结论证四边形BQDN是平行四边形,四边形GHQB是平行四边形,即可得到其数量关系.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∵AM,BN分别平分∠DAB,∠ABC,
∴∠MAB+∠NBA=![]() (∠DAB+∠ABC)=×180°=90°.
(∠DAB+∠ABC)=×180°=90°.
∴∠EGF=∠AGB=90°,
同理:∠EHF=90°,∠GEH=90°,
∴四边形EHFG是矩形;
(2)ABCD满足∠BAD=90°,且BC=2AB时,四边形EHFG为正方形;理由如下:
此时F点落在AD边上,与点P、点N重合,如图1所示:
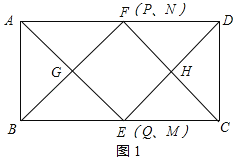
由(1)得:四边形EHFG是矩形,AG⊥BN,
∵AD∥BC,
∴∠AFB=∠CBF,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠AFB=∠ABF,
∴AF=AB,
同理:DF=CD,
∴AF=AB=BE,
∵∠BAD=90°,
∴△BAF、△ABE是等腰直角三角形,
∵AE⊥BF,
∴BG=FG,AG=EG,
∴AG=![]() BF=BG=FG,
BF=BG=FG,
∴FG=EG,
∴四边形EHFG为正方形,
故答案为:∠BAD=90°,且BC=2AB;
ABCD满足BC=2AB时,F点落在AD边上.(与点P、点N重合);理由如下:
如图2所示:
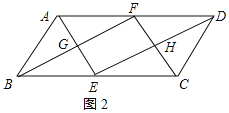
由(1)得:AF=AB,DF=CD,AG⊥BN,
∴AF=DF=AB,
∴AD=2AB,
∴BC=2AB,
故答案为:BC=2AB;
(3)矩形EHFG的对角线长度与ABCD的边长之间的数量关系为GH=BC﹣AB;理由如下:如图3所示:连接EF、GH
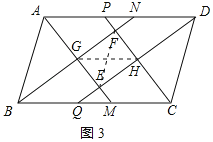
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∵四边形EHFG是矩形,
∴GH=EF,BN∥DQ,
∴四边形BQDN是平行四边形,
∴BN=DQ,
同(1)(2)得:AG⊥BN,AN=AB,CQ=CD=AB,
∴BG=NG,
同理:
∴BG=QH,
∴四边形GHQB是平行四边形,
∴GH=BQ=BC﹣CQ=BC﹣AB.
-
科目: 来源: 题型:
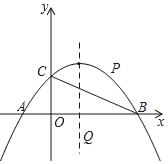
查看答案和解析>>【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+k+1的图象与一次函数y=﹣x+4的图象交于点A(1,a).

(1)求a、k的值;
(2)根据图象,写出不等式﹣x+4>kx+k+1的解;
(3)结合图形,当x>2时,求一次函数y=﹣x+4函数值y的取值范围;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了
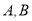 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息. .
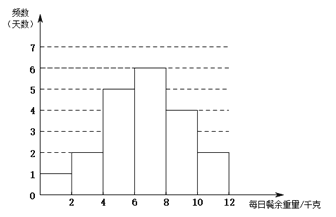
.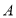 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组: ,
, ,
,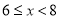 ,
,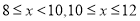 ):
):
 .
. 部门每日餐余重量在
部门每日餐余重量在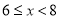 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8 .
.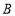 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8 .
.  两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:部门
平均数
中位数
众数
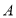
6.4
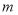
7.0
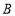 /p>
/p>6.6
7.2

根据以上信息,回答下列问题:
(1)写出表
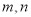 中的值;
中的值;(2)在
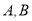 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“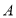 ”或“
”或“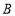 ”),理由是____________;
”),理由是____________;(3)结合
 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量. -
科目: 来源: 题型:
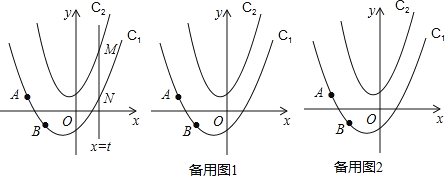
查看答案和解析>>【题目】如图,在平面角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表示线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;
(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点k,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时,请直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
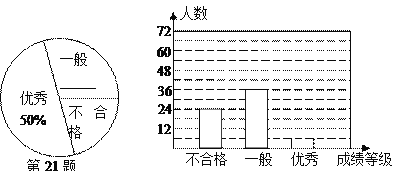
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车同时从
 城出发驶向
城出发驶向 城,甲车到达
城,甲车到达 城后立即返回.如图它们离
城后立即返回.如图它们离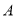 城的距离
城的距离 (千米)与行驶时间
(千米)与行驶时间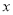 (小时)之间的函数图象.
(小时)之间的函数图象.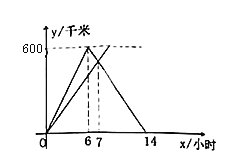
(1)求甲车行驶过程中
 与
与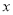 的函数解析式,并写出自变量
的函数解析式,并写出自变量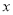 的取值范围;
的取值范围;(2)求相遇时间和乙车速度;
(3)在什么时间段内甲车在乙车前面?
相关试题

