搜索
【题目】甲、乙两车同时从
城出发驶向
城，甲车到达城后立即返回.如图它们离城的距离
(千米)与行驶时间
(小时)之间的函数图象.
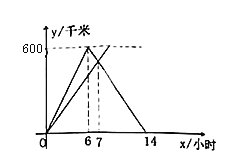
（1）求甲车行驶过程中与的函数解析式，并写出自变量的取值范围；
（2）求相遇时间和乙车速度；
（3）在什么时间段内甲车在乙车前面?
参考答案：
【答案】（1）甲由A城到B城关系式为：
返程关系式为 ：
（2）相遇时间为7小时，乙的车速为75千米/小时 （3）0-7小时时间段内甲车在乙车前面
【解析】
（1）设甲行驶中正比例函数
,将（6,600）代入即可求得
；设甲的返程函数式
为把（6,600）和（14,0）代入求得
(2)根据图像得出甲乙相遇时间为7小时，再把x=7代入甲返程所得函数关系式解得离A城的距离，即可求出乙的速度
（3）由图像即可得出答案
解：（1）设甲由A城到B城行驶过程关系式为
将（6,600）代入，求得=100，
所以由A城到B城行驶过程关系式为
设甲由B城到A城行驶过程关系式为
把（6,600）和（14,0）代入求得=-75
所以甲返程关系式为
（2）有图像可知两车相遇时间为7小时
当x=7时代入解得y=525
所以乙的速度为
（3）由图像可知在0—7小时内甲车在乙车前面.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AD＞AB，AM、BN、CP、DQ为四个内角的角平分线，P、为AD边上两点，其中AM与DQ相交于E，BN与CP相交于F，AM与BN相交于G，CP与DQ相交于H．
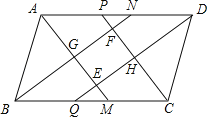
（1）求证：四边形EHFG是矩形．
（2）ABCD满足 时，四边形EHFG为正方形；ABCD满足 时，F点落在AD边上．（与点P、点N重合）
（3）探究矩形EHFG的对角线长度与ABCD的边长之间的数量关系，并证明．
-
科目： 来源： 题型：
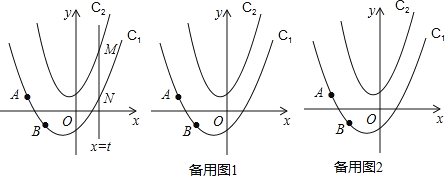
查看答案和解析>>【题目】如图，在平面角坐标系中，抛物线C1：y=ax2+bx﹣1经过点A（﹣2，1）和点B（﹣1，﹣1），抛物线C2：y=2x2+x+1，动直线x=t与抛物线C1交于点N，与抛物线C2交于点M．
（1）求抛物线C1的表达式；
（2）直接用含t的代数式表示线段MN的长；
（3）当△AMN是以MN为直角边的等腰直角三角形时，求t的值；
（4）在（3）的条件下，设抛物线C1与y轴交于点P，点M在y轴右侧的抛物线C2上，连接AM交y轴于点k，连接KN，在平面内有一点Q，连接KQ和QN，当KQ=1且∠KNQ=∠BNP时，请直接写出点Q的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（11·漳州）（满分8分）漳州市某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图（不完整）．请你根据图中所给的信息解答下列问题：
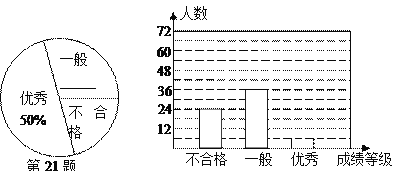
（1）请将以上两幅统计图补充完整；
（2）若“一般”和“优秀”均被视为达标成绩，则该校被抽取的学生中有_ ▲ 人达标；
（3）若该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．
（1）求抛物线的解析式；
（2）当点P运动到什么位置时，△PAB的面积有最大值？
（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地为了鼓励居民节约用水，决定实行两级收费制，即每月用水量不超过12吨（含12吨）时，每吨按政府补贴优惠价收费；每月超过12吨，超过部分每吨按市场调节价收费，小黄家1月份用水24吨，交水费42元．2月份用水20吨，交水费32元．
（1）求每吨水的政府补贴优惠价和市场调节价分别是多少元；
（2）设每月用水量为
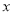吨，应交水费为
元，写出
与
之间的函数关系式；（3）小黄家3月份用水26吨，他家应交水费多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克)
不超过20千克
20千克以上但不超过40千克
40千克以上
每千克的价格
6元
5元
4元
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?
相关试题
