【题目】如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=5,CE=4,则⊙O的半径是________.

参考答案:
【答案】![]()
【解析】如图所示:连接OD、BD,
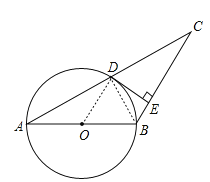
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD⊥AC,
又∵AB=BC,
∴AD=CD,
又∵AO=OB,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE是⊙O的切线,
∴DE⊥OD,
∴DE⊥BC,
∵CD=5,CE=4,
∴DE=![]() =3,
=3,
∵S△BCD=BDCD÷2=BCDE÷2,
∴5BD=3BC,
∴BD=![]() BC,
BC,
∵BD2+CD2=BC2,
∴(![]() BC)2+52=BC2,
BC)2+52=BC2,
解得BC=![]() ,
,
∵AB=BC,
∴AB=![]() ,
,
∴⊙O的半径是: ![]() ÷2=
÷2=![]() .
.
故答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=24,BC=12,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠ABC=30°,AE⊥BC于E,AF⊥CD于F,已知BE=
 ,CF=1,则AC=_____.
,CF=1,则AC=_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别是ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求
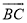 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】网上销售已成为产品销售的一种重要方式,很多大学生也在网上开起了网店,某手机销售网店正在代理销售一种新型智能手机,手机每部进价为1000元,经过试销发现:售价x(元/部)与每天交易量y(部)之间满足如图所示关系。
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售价x之间的函数关系式.若你是网店老板,会将价格定为多少,使每天获得的利润最大,最大利润是多少?

相关试题

