【题目】如图,在矩形ABCD中,AB=24,BC=12,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为_____.

参考答案:
【答案】90
【解析】
证得∠CAF=∠FCA,则AF=CF,设AF=x,则在Rt△BCF中,根据勾股定理求x,于是得到AF=AB-BF,即可得到结果.
∵四边形ABCD是矩形,
∴AB=CD=24,AD=BC=12,DC∥AB,
∴∠DCA=∠CAF,
由折叠得:∠DCA=∠D′CA,
∴∠CAF=∠FCA,
∴AF=CF,
设AF=x=FC,则BF=24﹣x,
在Rt△BCF中,由勾股定理得:(24﹣x)2+122=x2,
解得:x=15,
∴重叠部分的面积:S△AFC=![]() ×15×12=90,
×15×12=90,
故答案为:90.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求值1+2+22+23+24+…+22014
解:设S=1+2+22+23+24+…+22014 ①,将等式两边同时乘以2得
2S=2+22+23+24+…+22014+22015 ②
将②﹣①得:S=22015﹣1,即S=1+2+22+23+24+…+22014=22015﹣1
请你仿照此法计算:
(1)1+3+32+33+…+3100
(2)1+
 +
+ +
+ +…+
+…+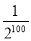 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,∠ABC=30°,AE⊥BC于E,AF⊥CD于F,已知BE=
 ,CF=1,则AC=_____.
,CF=1,则AC=_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=5,CE=4,则⊙O的半径是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别是ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.

相关试题

