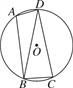
【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)π.
【解析】试题分析: ![]() 根据圆内接四边形的对角互补,∠DCB+∠BAD=180°,即可求出
根据圆内接四边形的对角互补,∠DCB+∠BAD=180°,即可求出
![]() 的度数,得出
的度数,得出![]() ,根据等角对等边即可证明.
,根据等角对等边即可证明.
![]() 求出
求出![]() 的度数,根据弧长公式计算即可.
的度数,根据弧长公式计算即可.
试题解析:
![]() 证明:∵四边形ABCD内接于圆O,
证明:∵四边形ABCD内接于圆O,
∴∠DCB+∠BAD=180°.
∵∠BAD=105°,
∴∠DCB=180°-105°=75°.
∵∠DBC=75°,
∴∠DCB=∠DBC=75°,
∴BD=CD;
(2)∵∠DCB=∠DBC=75°,
∴∠BDC=30°,
由圆周角定理,得![]() 的度数为60°,
的度数为60°,
故![]() 的长为:
的长为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③S△ABF:S四边形CDEF=2:5;④cos∠CAD=
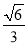 .其中正确的结论有( ).
.其中正确的结论有( ).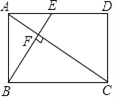
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
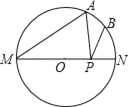
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=2a,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则 PA+PB的最小值为_____.(用含a的代数式表示)
-
科目: 来源: 题型:
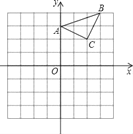
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1.
(2)点C1的坐标为( , ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)比较大小:
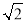 +1
+1 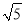 (填“>”、“<”或者“ =”)
(填“>”、“<”或者“ =”)(2)其实我们可以利用三角形的知识在方格纸上画图验证⑴的结果,请在图①中画出相应的图形(设小正方形的边长为1)

(3)请用(2)中的方法在图②中画图比较大小:
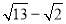
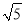
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一矩形纸片
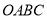 放在直角坐标系中,
放在直角坐标系中,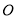 为原点,点
为原点,点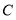 在
在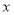 轴上,点
轴上,点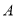 在
在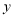 轴上,
轴上,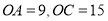 .
.(1)如图1,在
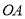 上取一点
上取一点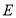 ,将
,将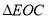 沿
沿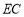 折叠,使
折叠,使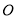 点落在
点落在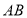 边上的
边上的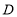 点处,求直线
点处,求直线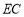 的解析式;
的解析式;(2)如图2,在
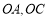 边上选取适当的点
边上选取适当的点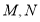 ,将
,将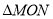 沿
沿 折叠,使
折叠,使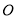 点落在
点落在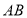 边上的点
边上的点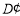 处,过
处,过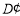 作
作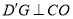 于点
于点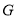 ,交
,交 于
于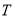 点,连接
点,连接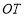 ,判断四边形
,判断四边形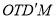 的形状,并说明理由;
的形状,并说明理由;(3)、在(2)的条件下,若点
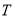 坐标
坐标 ,点
,点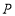 在
在 直线上,问坐标轴上是否存在点
直线上,问坐标轴上是否存在点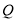 ,使以
,使以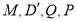 为顶点的四边形是平行四边形,若存在,请直接写出点
为顶点的四边形是平行四边形,若存在,请直接写出点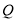 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.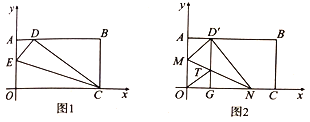
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有单人间、双人间和三人间三种客房供游客租住,某旅行团有18人准备同时租用这三种客房共9间,且每个房间都住满,则租房方案共有______种.
相关试题

