【题目】在ABCD中,∠ABC=30°,AE⊥BC于E,AF⊥CD于F,已知BE=![]() ,CF=1,则AC=_____.
,CF=1,则AC=_____.
参考答案:
【答案】![]() 或2.
或2.
【解析】
分当F在线段CD上时和F在线段DC的延长线上两种情况分别运用平行四边形的性质、直角三角形的性质和解直角三角形的知识解答即可.
解:①如图1中,当F在线段CD上时
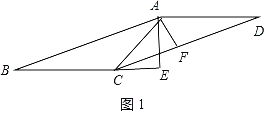
∵ABCD
∴AB=CD
在Rt△ABE中,
∵∠B=30°,BE=![]() ,∠AEB=90°,
,∠AEB=90°,
∴AE=1,AB=2,
∵CF=1,AB=CD=2,
∴DF=CF=1,
∵AF⊥CD,
∴AC=AD,
在Rt△ADF中,∠D=30°,cos30°=![]() ,
,
∴AD=![]() ,
,
∴AC=![]() ,
,
②当F在线段DC的延长线上时
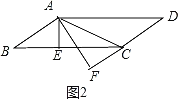
在Rt△ABE中,∵∠B=30°,BE=![]() ,∠AEB=90°,
,∠AEB=90°,
∴AE=1,AB=2,
∵CF=1,AB=CD=2,
∴DF=3,
∵AF⊥CD,∠D=∠B=30°,
∴AD=BC=2![]() ,
,
∴BE=EC,
∵AE⊥BC,
∴AC=AB=2,
故答案为![]() 或2.
或2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;
②方程
 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=24,BC=12,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E,若CD=5,CE=4,则⊙O的半径是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别是ABCD的边BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=8,∠BAC=90°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求
 的长.
的长.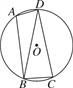
相关试题

