【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

参考答案:
【答案】(1)BD=1m;(2)CE与BE的大小关系是CE=BE,证明见解析.
【解析】
(1)利用勾股定理求出OB,求出OC,再根据勾股定理求出OD,即可求出答案;
(2)求出△AOB和△DOC全等,根据全等三角形的性质得出OC=OB,∠ABO=∠DCO,求出∠OCB=∠OBC,求出∠EBC=∠ECB,根据等腰三角形的判定得出即可.
(1)∵AO⊥OD,AO=4m,AB=5m,
∴OB=![]() =3m,
=3m,
∵梯子的顶端A沿墙下滑1m至C点,
∴OC=AO﹣AC=3m,
∵CD=AB=5m,
∴由勾股定理得:OD=4m,
∴BD=OD﹣OB=4m﹣3m=1m;
(2)CE与BE的大小关系是CE=BE,证明如下:
连接CB,由(1)知:AO=DO=4m,AB=CD=5m,
∵∠AOB=∠DOC=90°,
在Rt△AOB和Rt△DOC中
![]() ,
,
∴Rt△AOB≌Rt△DOC(HL),
∴∠ABO=∠DCO,OC=OB,
∴∠OCB=∠OBC,
∴∠ABO﹣∠OBC=∠DCO﹣∠OCB,
∴∠EBC=∠ECB,
∴CE=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)请在数轴上标出下列各数,按从小到大的顺序排列,并用“<”号连接:
2,﹣2
 ,﹣
,﹣ ,0.5;
,0.5;
(2)有理数a、b在数轴上的位置如图所示:

化简:|a|= ,|﹣b|= ,|1+a|= ,|1﹣b|= .
-
科目: 来源: 题型:
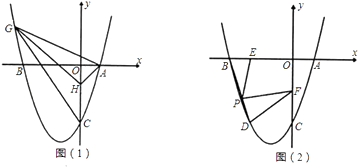
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3).
(1)求抛物线的解析式;
(2)如图(1),己知点H(0,﹣1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(﹣2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=ax2+bx+a+b(a≠0)的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A和点F,点B和点E分别是反比例函数y=
 图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 .
图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时)
0
1
2
2.5
余油量y(升)
100
80
60
50
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

相关试题

