【题目】函数y=ax2+bx+a+b(a≠0)的图象可能是( )
A.
B.
C.
D.
参考答案:
【答案】C
【解析】解:A:由图象可知,开口向下,则a<0,又因为顶点在y轴左侧,则b<0,则a+b<0,而图象与y轴交点为(0,a+b)在y轴正半轴,与a+b<0矛盾,故此选项错误; B:由图象可知,开口向下,则a<0,又因为顶点在y轴左侧,则b<0,则a+b<0,而图象与y轴交点为(0,1)在y轴正半轴,可知a+b=1与a+b<0矛盾,故此选项错误;
C:由图象可知,开口向上,则a>0,顶点在y轴右侧,则b<0,a+b=1,故此选项正确;
D:由图象可知,开口向上,则a>0,顶点在y轴右侧,则b<0,与y轴交于正半轴,则a+b>0,而图象与x轴的交点为(1,0),则a+b+a+b=0,即a+b=0与a+b>0矛盾,故此选项错误.
故选C.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
销售方式
粗加工后销售
精加工后销售
每吨获利(元)
1000
2000
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工. ①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)请在数轴上标出下列各数,按从小到大的顺序排列,并用“<”号连接:
2,﹣2
 ,﹣
,﹣ ,0.5;
,0.5;
(2)有理数a、b在数轴上的位置如图所示:

化简:|a|= ,|﹣b|= ,|1+a|= ,|1﹣b|= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3).
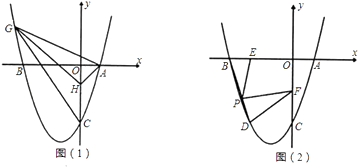
(1)求抛物线的解析式;
(2)如图(1),己知点H(0,﹣1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(﹣2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A和点F,点B和点E分别是反比例函数y=
 图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 .
图象在第一象限和第三象限上的点,过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为点C、D,CD=6,且AF=FC,DE=BE,已知四边形ADCF的面积是四边形BCDE的面积的2倍,则OC的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时)
0
1
2
2.5
余油量y(升)
100
80
60
50
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?
相关试题

