【题目】已知:如图,在![]() 中,
中,![]() 是
是![]() 边上的一点,
边上的一点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行交
的平行交![]() 延长点
延长点![]() ,且
,且![]() ,连接
,连接![]() .
.

(1)求证:![]() 是
是![]() 的中点;
的中点;
(2)若![]() ,试判断四边形
,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
参考答案:
【答案】(1)见解析;(2)四边形ADCF是菱形,证明见解析
【解析】
(1)先通过AAS证得△AEF≌△DEB进而可得AF=DB,再结合AF=DC作等量代换即可;
(2)先通过AF∥DC,AF=DC证得四边形ADCF是平行四边形,再结合邻边相等即可得证.
证明:(1)∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB,
∴AF=DB,
∵AF=DC,
∴DB=DC,
∴D是BC的中点,
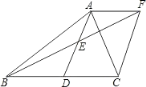
(2)四边形ADCF是菱形,
证明:∵AF∥DC,AF=DC,
∴四边形ADCF是平行四边形,
∵AD=BD,DB=DC,
∴AD=DC,
∴□ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区果农收获草莓30吨,枇杷13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往省城,已知甲种货车可装草莓4吨和枇杷1吨,乙种货车可装草莓、枇杷各2吨.
(1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来;
(2)若甲种货车每辆要付运输费2 000元,乙种货车每辆要付运输费1 300元,则该果农应选择哪种运输方案才能使运费最少,最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
 =
=  =
=  ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=  ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
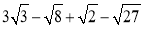 .
.(2)计算:
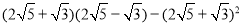 .
.(3)已知
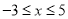 ,求:
,求: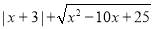 的值.
的值.(4)如图,在四边形
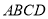 中,
中,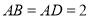 ,
, ,
, ,
,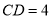 ,求
,求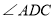 的度数.
的度数.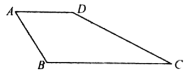
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4
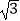 ,则S阴影=( )
,则S阴影=( ) 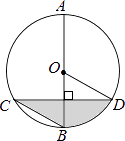
A.2π??
B. π??
π??
C. π??
π??
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、AD是⊙O的弦,点C是DO的延长线与弦AB的交点,∠ABO=30°,OB=2.

(1)求弦AB的长;
(2)若∠D=20°,求∠BOD的度数. -
科目: 来源: 题型:
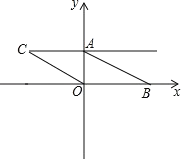
查看答案和解析>>【题目】如图.已知在平面直角坐标系中.点 A(0,m),点 B(n,0),D(2m,n),且 m、n 满足(m﹣2)2+
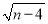 =0,将线段AB向左平移,使点B与点 O重合,点C与点A对应.
=0,将线段AB向左平移,使点B与点 O重合,点C与点A对应. (1)求点C、D的坐标;
(2)连接CD,动点P从点O出发,以每秒1个单位的速度,沿射线OB方向运动,设点P运动时间为t秒,是否存在某一时刻,使 SPCD=4SAOB,若存在,请求出t值,并写出P点坐标;若不存在,请说明理由.
相关试题

