【题目】(1)计算:![]() .
.
(2)计算:![]() .
.
(3)已知![]() ,求:
,求:![]() 的值.
的值.
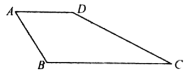
(4)如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
参考答案:
【答案】(1)![]() ;(2)-6-4
;(2)-6-4![]() ;(3)8;(4)150°
;(3)8;(4)150°
【解析】
(1)利用二次根式的乘法法则和加减法法则计算即可;
(2)利用平方差公式和完全平方公式计算即可;
(3)利用二次根式的性质和绝对值的代数意义化简即可;
(4)连接BD,先证△ABD为等边三角形,再用勾股定理的逆定理证得△BCD为直角三角形且∠BDC=90°即可.
解:(1)原式=3![]() -2
-2![]() +
+![]() -3
-3![]()
=-![]()
(2)原式=20-3-(20+3+4![]() )
)
=17-23-4![]()
=-6-4![]()
(3)原式=![]() +3+
+3+![]()
=![]() +3+5-
+3+5-![]()
=8
(4)如图,连接BD,

∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,DB=AD=2,
∵BC=2![]() ,CD=4,DB=2,
,CD=4,DB=2,
∴DB2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=60°+90°=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、C是⊙A上的两点,AB的垂直平分线与⊙A交于E、F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=( )

A.30°
B.29°
C.28°
D.20° -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区果农收获草莓30吨,枇杷13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往省城,已知甲种货车可装草莓4吨和枇杷1吨,乙种货车可装草莓、枇杷各2吨.
(1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来;
(2)若甲种货车每辆要付运输费2 000元,乙种货车每辆要付运输费1 300元,则该果农应选择哪种运输方案才能使运费最少,最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
 =
=  =
=  ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=  ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的平行交
的平行交 延长点
延长点 ,且
,且 ,连接
,连接 .
.
(1)求证:
 是
是 的中点;
的中点;(2)若
 ,试判断四边形
,试判断四边形 的形状,并证明你的结论.
的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4
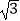 ,则S阴影=( )
,则S阴影=( ) 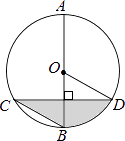
A.2π??
B. π??
π??
C. π??
π??
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、AD是⊙O的弦,点C是DO的延长线与弦AB的交点,∠ABO=30°,OB=2.

(1)求弦AB的长;
(2)若∠D=20°,求∠BOD的度数.
相关试题

