【题目】如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ![]() ,则S阴影=( )
,则S阴影=( ) 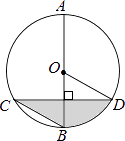
A.2π??
B.![]() π??
π??
C.![]() π??
π??
D.![]() π
π
参考答案:
【答案】B
【解析】解:如图,假设线段CD、AB交于点E, 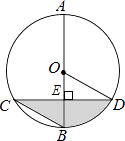
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED=2 ![]() ,
,
又∵∠BCD=30°,
∴∠DOE=2∠BCD=60°,∠ODE=30°,
∴OE=DEcot60°=2 ![]() ×
× ![]() =2,OD=2OE=4,
=2,OD=2OE=4,
∴S阴影=S扇形ODB﹣S△DOE+S△BEC= ![]() ﹣
﹣ ![]() OE×DE+
OE×DE+ ![]() BECE=
BECE= ![]() ﹣2
﹣2 ![]() +2
+2 ![]() =
= ![]() .
.
故选B.
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
 =
=  =
=  ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=  ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
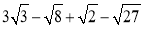 .
.(2)计算:
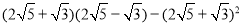 .
.(3)已知
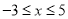 ,求:
,求: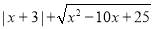 的值.
的值.(4)如图,在四边形
 中,
中,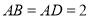 ,
, ,
, ,
,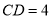 ,求
,求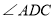 的度数.
的度数.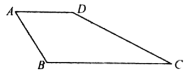
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的平行交
的平行交 延长点
延长点 ,且
,且 ,连接
,连接 .
.
(1)求证:
 是
是 的中点;
的中点;(2)若
 ,试判断四边形
,试判断四边形 的形状,并证明你的结论.
的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB、AD是⊙O的弦,点C是DO的延长线与弦AB的交点,∠ABO=30°,OB=2.

(1)求弦AB的长;
(2)若∠D=20°,求∠BOD的度数. -
科目: 来源: 题型:
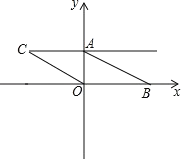
查看答案和解析>>【题目】如图.已知在平面直角坐标系中.点 A(0,m),点 B(n,0),D(2m,n),且 m、n 满足(m﹣2)2+
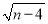 =0,将线段AB向左平移,使点B与点 O重合,点C与点A对应.
=0,将线段AB向左平移,使点B与点 O重合,点C与点A对应. (1)求点C、D的坐标;
(2)连接CD,动点P从点O出发,以每秒1个单位的速度,沿射线OB方向运动,设点P运动时间为t秒,是否存在某一时刻,使 SPCD=4SAOB,若存在,请求出t值,并写出P点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是直立在高速公路边水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为( )
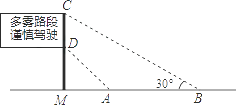
A.4 米
米
B.(2 +2)米
+2)米
C.(4 ﹣4)米
﹣4)米
D.(4 ﹣4)米
﹣4)米
相关试题

