【题目】如图是小明从学校到家里行进的路程![]() (米)与时间
(米)与时间![]() (分)的函数图象.给出以下结论:①学校离小明家
(分)的函数图象.给出以下结论:①学校离小明家![]() 米;②小明用了
米;②小明用了![]() 分钟到家;③小明前
分钟到家;③小明前![]() 分钟走了整个路程的一半;④小明后
分钟走了整个路程的一半;④小明后![]() 分钟比前
分钟比前![]() 分钟走得快.其中正确结论的个数是( )
分钟走得快.其中正确结论的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
根据图象的纵坐标,可判断①,根据图象的横坐标,可判断②,结合图象的横坐标、纵坐标,可判断③④,综上即可得答案.
①由图象的纵坐标可以看出学校离小明家1000米,故①正确,
②由图象的横坐标可以看出小明用了20到家,故②正确,
③由图象的横、纵横坐标可以看出,小明前10分钟走的路程较少,故③错误,
④由图象的横、纵横坐标可以看出,小明后10分钟比前10分钟走的路程多,所以后10分钟比前10分钟走得快,故④正确,
综上所述:正确的结论有①②④共三个,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有人喜欢把传送的便条折成“
 ”形状,折叠过程按图
”形状,折叠过程按图 的顺序进行(其中阴影部分表示纸条的反面):
的顺序进行(其中阴影部分表示纸条的反面): 
如果由信纸折成的长方形纸条(图①)长
 厘米,分别回答下列问题:
厘米,分别回答下列问题:(1)如图①、图②,如果长方形纸条的宽为
 厘米,并且开始折叠时
厘米,并且开始折叠时 厘米,那么在图②中,
厘米,那么在图②中, ____厘米.
____厘米.(2)如图②,如果长方形纸条的宽为
 厘米,现在不但要折成图②的形状,还希望纸条两端超出点
厘米,现在不但要折成图②的形状,还希望纸条两端超出点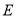 的部分
的部分 和
和 相等,使图②. 是轴对称图形,
相等,使图②. 是轴对称图形, ______厘米.
______厘米.(3)如图④,如果长方形纸条的宽为
 厘米,希望纸条两端超出点
厘米,希望纸条两端超出点 的部分
的部分 和
和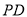 相等,即最终图形是轴对称图形,试求在开始折叠时起点
相等,即最终图形是轴对称图形,试求在开始折叠时起点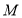 与点
与点 的距离(结果用
的距离(结果用 表示) .
表示) . -
科目: 来源: 题型:
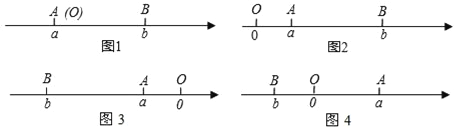
查看答案和解析>>【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数
 的图象经过点
的图象经过点 ,则这个一次函数( )
,则这个一次函数( )A.
 随
随 的增大而增大B.
的增大而增大B. 随
随 的增大而减小
的增大而减小C.图象经过原点D.图象与坐标轴围成的三角形的面积为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
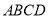 中,点
中,点 、
、 、
、 分别是
分别是 、
、 、
、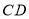 的中点,
的中点, 、
、 交于
交于 ,连接
,连接 、
、 .下列结论:①
.下列结论:① ;②
;② ;③
;③ ;④
;④ .正确的有( )
.正确的有( )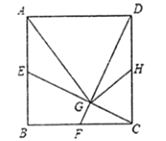
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为 ;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=
 AB,求折痕MN的长;
AB,求折痕MN的长;问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.

相关试题

