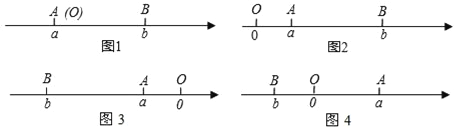
【题目】阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
参考答案:
【答案】(1)3;3;7;(2)|x+1|,1或﹣3;(3)4.
【解析】试题分析:(1)数轴上表示2和5的两点之间的距离是|5-2|=3,-2和-5的两点之间的距离是|-2-(-5)|=3,表示-2和5的两点之间的距离是|5-(-2)|=7;(2)数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,令|x+1|=2,解得x=1或-3;(3)代数式|x-1|+|x+3|表示数轴上一点到1、-3两点的距离的和,根据两点之间线段最短可知,有最小值为:1-(-3)=4.
试题解析:
(1)数轴上表示2和5的两点之间的距离是:|5-2|=3,
数轴上表示-2和-5的两点之间的距离是|-2-(-5)|=3,
数轴上表示-2和5的两点之间的距离是|5-(-2)|=7;
(2)数轴上表示x和-1的两点之间的距离是|x+1|,|AB|=2,则|x+1|=2,故x=1或-3;
(3)代数式|x-1|+|x+3|表示数轴上一点到1、-3两点的距离的和,根据两点之间线段最短可知,有最小值为:1-(-3)=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.

(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为
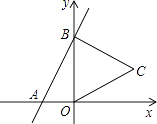
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长为4,8,则第三边的长度可以是 (写出一个即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x (元)
15
20
25
…
y (件)
25
20
15
…
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)求销售价定为30元时,每日的销售利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】把方程3x2+x=5x﹣2整理成一元二次方程的一般形式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.求原计划每天加工多少套运动服?
相关试题

