【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为 ;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=![]() AB,求折痕MN的长;
AB,求折痕MN的长;
问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.

参考答案:
【答案】(1)2;
(2)MN的长为![]() .
.
(3)折痕的长为5或![]() .
.
【解析】(1)如图1中,B的对称点B/,折痕为MN,MN交BB/于H. 只要证明折痕是△ABC的中位线即可.
(2)如图2中,B的对称点B/,折痕为MN,MN交BB/于H,求出直线MN的解析式即可解决问题.
(3)存在. 如图3中,延长BQ交OA于B//,连接AQ,过点作Q作MN∥OA,交OC于M,交AB于N,可以证明线段MN计算折痕;作BB//的垂直平分线PF,交OC于P,交AB于F,此时B、B//关于直线PF对称,线段PF也是折痕,分别求出MN、PF即可解决问题.
解:(1)如图1中,B的对称点B′,
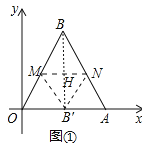
折痕为MN,MN交BB′于H.
∵△ABC是等边三角形,OB′=B′A,∴BB′⊥OA,又∵BB′⊥MN,
∴MN∥OA,∵BH=HB′,∴BM=OM,BN=NA,
∴MN是△ABC的中位线,∴MN=![]() OA=2.故答案为2.
OA=2.故答案为2.
(2)如图2中,B的对称点B′,折痕为MN,MN交BB′于H
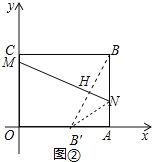
∵AN=![]() AB=2,∴NB=NB′=4,
AB=2,∴NB=NB′=4,
在Rt△ANB′中,AB′=![]() =2
=2![]() ,∴OB′=8﹣2
,∴OB′=8﹣2![]() ,
,
∴点B′(8﹣2![]() ,0),∵B(8,6),
,0),∵B(8,6),
∴BB′中点H(8﹣![]() ,3),∵点N坐标(8,2),
,3),∵点N坐标(8,2),
设直线NH解析式为y=kx+b,则有![]() 解得
解得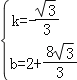 ,
,
∴直线NH解析式为y=﹣![]() x+2+
x+2+![]() ,∴点M坐标(0,2+
,∴点M坐标(0,2+![]() ),
),
∴MN=![]() =
=![]() .
.

(3)存在.理由:如图3中,延长BQ交OA于B″,连接AQ,过点Q作MN∥OA,交OC于M,交AB于N.
∵Q(4,3),∴N(6,3),∴BN=AN.QB=QB″,
作BB″的垂直平分线PF,交OC于P,交AB于F,此时B、B″关于直线PF对称,满足条件,
在Rt△ABB″中,∵∠BAB″=90°,BQ=QB″,∴AQ=QB,
∴此时B、A(B′)关于直线MN对称,满足条件.∵C(2,6),
∴直线OC解析式为y=3x,∵NM∥OA,BN=NA,∴CM=OM,∴点M(1,3),
∴MN=5,∵B(6,6),B″(2,0),∴可得直线BB″的解析式为y=![]() x﹣3,
x﹣3,
∴过点Q垂直BB″的直线PF的解析式为y=﹣![]() x+
x+![]() ,
,
由 解得
解得![]() ,∴点P(
,∴点P(![]() ,
,![]() ),F(6,
),F(6,![]() ),
),
∴PF=![]() =
=![]() ,综上所述,折痕的长为5或
,综上所述,折痕的长为5或![]() .
.
“点睛”本题考查四边形综合题、一次函数、勾股定理、线段垂直平分线性质,两条直线垂直k的乘积为-1等知识,解题的关键是灵活待定系数法确定函数解析式,学会利用解方程组求两个函数的交点坐标,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
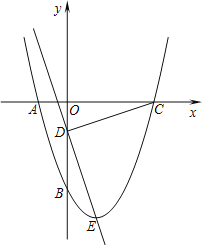
查看答案和解析>>【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(-8)2018×0.1252017=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
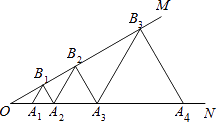
A.8
B.16
C.24
D.32 -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一边的夹角为80°,则顶角的度数为 .
-
科目: 来源: 题型:
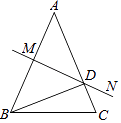
查看答案和解析>>【题目】如图,已知AB=AC,∠A=40°,AB=10,DC=3,AB的垂直平分线MN交AC于点D,则∠DBC=度,BD= .
相关试题

