【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
参考答案:
【答案】A
【解析】
只要证明△DAB≌△EAC,利用全等三角形的性质即可一一判断;
∵∠DAE=∠BAC=90°,
∴∠DAB=∠EAC
∵AD=AE,AB=AC,
∴△DAB≌△EAC,
∴BD=CE,∠ABD=∠ECA,故①正确,
∴∠ABD+∠ECB=∠ECA+∠ECB=∠ACB=45°,故②正确,
∵∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=45°+45°=90°,
∴∠CEB=90°,即CE⊥BD,故③正确,
∴BE2=BC2-EC2=2AB2-(CD2-DE2)=2AB2-CD2+2AD2=2(AD2+AB2)-CD2.故④正确,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数
 的图象经过点
的图象经过点 ,则这个一次函数( )
,则这个一次函数( )A.
 随
随 的增大而增大B.
的增大而增大B. 随
随 的增大而减小
的增大而减小C.图象经过原点D.图象与坐标轴围成的三角形的面积为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小明从学校到家里行进的路程
 (米)与时间
(米)与时间 (分)的函数图象.给出以下结论:①学校离小明家
(分)的函数图象.给出以下结论:①学校离小明家 米;②小明用了
米;②小明用了 分钟到家;③小明前
分钟到家;③小明前 分钟走了整个路程的一半;④小明后
分钟走了整个路程的一半;④小明后 分钟比前
分钟比前 分钟走得快.其中正确结论的个数是( )
分钟走得快.其中正确结论的个数是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
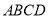 中,点
中,点 、
、 、
、 分别是
分别是 、
、 、
、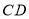 的中点,
的中点, 、
、 交于
交于 ,连接
,连接 、
、 .下列结论:①
.下列结论:① ;②
;② ;③
;③ ;④
;④ .正确的有( )
.正确的有( )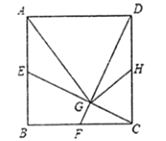
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为 ;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=
 AB,求折痕MN的长;
AB,求折痕MN的长;问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
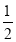 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( ) 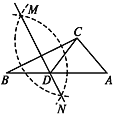
A. 90°B. 95°C. 100°D. 105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
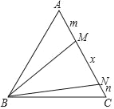
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随x,m,n的值而定
相关试题

