【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB= ![]() .
.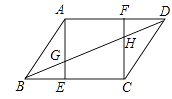
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
参考答案:
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴∠CDF=∠ABE,DC=AB= ![]() ,
,
∵tan∠ABE=2,
∴tan∠CDF=2,∵CF⊥AD,
∴△CFD是直角三角形,
∴ ![]() =2,设DF=x,则CF=2x,
=2,设DF=x,则CF=2x,
在Rt△CFD中,由勾股定理可得(2x)2+x2=( ![]() )2,
)2,
解得x=2或x=﹣2(舍去),
∴CF=4;
(2)解:证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵AE⊥BC,CF⊥AD,∴AE⊥AD,CF⊥BC,
∴∠GAD=∠HCB=90°,
∴△AGD≌△CHB,
∴BH=DG,
∴BG=DH.
【解析】(1)由平行四边形的性质,结合三角函数的定义,在Rt△CFD中,可求得CF=2DF,再利用勾股定理可求得CF的长。
(2)利用平行四边形的性质结合条件可证得△AGD≌△CHB,则可求得BH=DG,从而可证得BG=DH。
-
科目: 来源: 题型:
查看答案和解析>>【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠BAC=60°,点C在点B的正西方向,海岛B与灯塔C之间的距离是_____海里.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:

(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的边
的边 的中点,延长
的中点,延长 交
交 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)若
 ,
, ,
, ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图和统计表(图中信息不完整).已知A、B两组捐款户数的比为1:5.请结合以上信息解答下列问题.捐款户数分组统计表
组别
捐款额(x)元
户数
A
1≤x<50
a
B
50≤x<100
10
C
100≤x<150
D
150≤x<200
E
x≥200
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计图1和捐款户数分组统计表”;
(3)若该社区有2000户住户,请根据以上信息,估计全社区捐款不少于150元的户数.
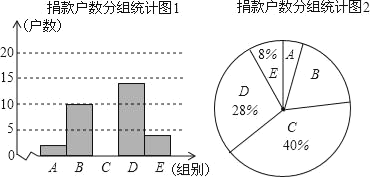
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果x=y,那么称这个四位数为“和平数”.
例如:2635,x=2+6,y=3+5,因为x=y,所以2635是“和平数”.
(1)请判断:3562 (填“是”或“不是”)“和平数”.
(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中, ,
, ,连接
,连接 ,
, ,点
,点 为
为 的中点,射线
的中点,射线 交
交 的延长线于点
的延长线于点 ,连接
,连接 .
.
(1)求证:四边形
 是菱形;
是菱形;(2)若
 ,
, ,求
,求 的长.
的长.
相关试题

