【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠BAC=60°,点C在点B的正西方向,海岛B与灯塔C之间的距离是_____海里.

参考答案:
【答案】30![]()
【解析】
由上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,可得AB=30海里,根据题意可得: △ABC是直角三角形,由∠BAC=60°,可得∠ACB=30°,根据在直角三角形中,30°所对直角边等于斜边的一半可得:AC=2AB=60海里,再根据勾股定理进行计算可得:BC=30![]() .
.
根据题意可得: △ABC是直角三角形,由∠BAC=60°,可得∠ACB=30°,
AB=2×15=30海里,
根据在直角三角形中30°所对直角边等于斜边的一半可得:
AC=2AB=60海里,
根据勾股定理可得:
BC=30![]() 海里,
海里,
故答案为: 30![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了6位战士,发现前面的人数和后面的人数一样.
(1)这列队伍一共有多少名战士?
(2)这列队伍要过一座320米的大桥,为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒,从第一位战士刚上桥到全体通过大桥用了100秒时间,请问相邻两个战士间距离为多少米(不考虑战士身材的大小)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们根据指数运算,得出了一种新的运算,如表是两种运算对应关系的一组实例:
指数运算
21=2
22=4
23=8
…
31=3
32=9
33=27
…
新运算
log22=1
log24=2
log28=3
…
log33=1
log39=2
log327=3
…
根据上表规律,某同学写出了三个式子:①log216=4,②log525=5,③log2
 =﹣1.其中正确的是( )
=﹣1.其中正确的是( )
A.①②
B.①③
C.②③
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
①当d=3时,m= ;
②当m=2时,d的取值范围是 .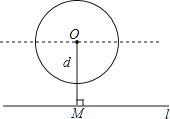
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产了台数相同A型、B型两种单价不同的计算机,B型机的单价比A型机的便宜0.24万元,已知A型机总价值120万元,B型计算机总价值为80万元,求A型、B型两种计算机的单价,设A型计算机的单价是x万元,可列方程_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二孩政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度,在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:
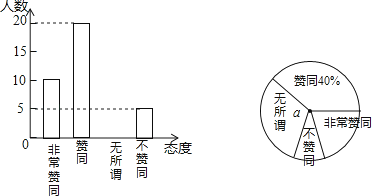
(1)在这次问卷调查中一共抽取了名学生,a=%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

相关试题

