【题目】如图是某月的月历,图中带阴影的方框恰好盖住四个数,不改变带阴影的方框的形状大小,移动方框的位置.
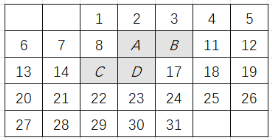
(1)若带阴影的方框盖住的4个数中,A表示的数是x,求这4个数的和(用含x的代数式表示);
(2)若带阴影的方框盖住的4个数之和为82,求出A表示的数;
(3)这4个数之和可能为38或112吗?如果可能,请求出这4个数,如果不可能,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ; (3) 不可能;不可能.
; (3) 不可能;不可能.
【解析】
(1) A表示的数是x,可知B表示的数是x+1,C表示的数是x+6,D表示的数是x+7,于是可耱这4个数的和;
(2) 令![]() =82,求出x即可;
=82,求出x即可;
(3) 令![]() =38,求出x=6,此时C超出方格,故不可能;令
=38,求出x=6,此时C超出方格,故不可能;令![]() =112,得x=24.5,因为x是整数,所以也不可能.
=112,得x=24.5,因为x是整数,所以也不可能.
解:(1) A表示的数是x,
∴B表示的数是x+1,C表示的数是x+6,D表示的数是x+7,
∴这4个数的和= x+x+1+x+6+x+7=![]() ;
;
(2) ![]() =82,
=82,
∴x=17,
∴A表示的数是17;
(3) 当![]() =38时,
=38时,
∴x=6,
∴此时C超出方格,
故不可能;
当![]() =112时,
=112时,
∴x=24.5,
∵x是整数,
∴故不可能.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动.发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点
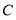 是线段
是线段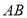 上的一点,
上的一点,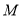 是
是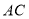 的中点,
的中点,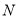 是
是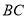 的中点.
的中点.
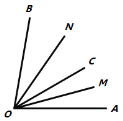
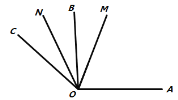
图1 图2 图3
(1)问题探究
①若
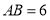 ,
,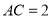 ,求
,求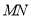 的长度;(写出计算过程)
的长度;(写出计算过程)②若
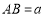 ,
,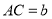 ,则
,则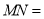 ___________;(直接写出结果)
___________;(直接写出结果)(2)继续探究
“创新”小组的同学类比想到:如图2,已知
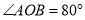 ,在角的内部作射线
,在角的内部作射线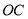 ,再分别作
,再分别作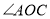 和
和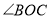 的角平分线
的角平分线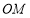 ,
,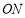 .
.③若
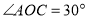 ,求
,求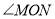 的度数;(写出计算过程)
的度数;(写出计算过程)④若
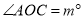 ,则
,则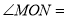 _____________
_____________ ;(直接写出结果)
;(直接写出结果)(3)深入探究
“慎密”小组在“创新”小组的基础上提出:如图3,若
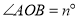 ,在角的外部作射线
,在角的外部作射线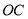 ,再分别作
,再分别作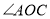 和
和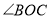 的角平分线
的角平分线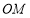 ,
,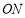 ,若
,若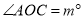 ,则
,则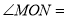 __________
__________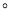 .(直接写出结果)
.(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】
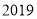 年
年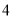 月
月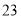 日是第
日是第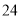 个世界读书日,为迎接第
个世界读书日,为迎接第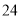 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;参赛者
推荐语
读书心得
读书讲座
甲
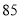
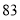
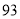
乙
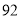
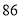
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按
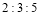 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由. -
科目: 来源: 题型:
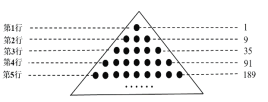
查看答案和解析>>【题目】如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右从小到大,且相邻两个点所表示的数相差1,每行数的和等于右边相应的数字,那么,表示2020的点在第______行,从左向右第______个位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB与直线CD相交于O,OB平分∠DOF.

(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(
 ),求∠AOE的度数(用含x的代数式表示).
),求∠AOE的度数(用含x的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, ,
, ,点
,点 是
是 边上的中点,点
边上的中点,点 是
是 上的一动点(不与点
上的一动点(不与点 重合),延长
重合),延长 交射线
交射线 于点
于点 ,连结
,连结 、
、 .
.
 求证:四边形
求证:四边形 是平行四边形;
是平行四边形; 填空:①当
填空:①当 ________时,四边形
________时,四边形 是矩形;②当
是矩形;②当 ________时,四边形
________时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
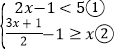
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为 .
相关试题

