【题目】综合与实践
问题情境
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动.发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点![]() 是线段
是线段![]() 上的一点,
上的一点,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
![]()
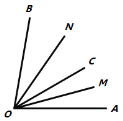
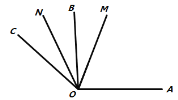
图1 图2 图3
(1)问题探究
①若![]() ,
,![]() ,求
,求![]() 的长度;(写出计算过程)
的长度;(写出计算过程)
②若![]() ,
,![]() ,则
,则![]() ___________;(直接写出结果)
___________;(直接写出结果)
(2)继续探究
“创新”小组的同学类比想到:如图2,已知![]() ,在角的内部作射线
,在角的内部作射线![]() ,再分别作
,再分别作![]() 和
和![]() 的角平分线
的角平分线![]() ,
,![]() .
.
③若![]() ,求
,求![]() 的度数;(写出计算过程)
的度数;(写出计算过程)
④若![]() ,则
,则![]() _____________
_____________![]() ;(直接写出结果)
;(直接写出结果)
(3)深入探究
“慎密”小组在“创新”小组的基础上提出:如图3,若![]() ,在角的外部作射线
,在角的外部作射线![]() ,再分别作
,再分别作![]() 和
和![]() 的角平分线
的角平分线![]() ,
,![]() ,若
,若![]() ,则
,则![]() __________
__________![]() .(直接写出结果)
.(直接写出结果)
参考答案:
【答案】(1)①3;②![]() ;(2)③40
;(2)③40![]() ;④40;(3)
;④40;(3)![]()
【解析】
(1)①先求出BC,再根据中点求出AM、BN,即可求出MN的长;
②利用①的方法求MN即可;
(2)③先求出∠BOC,再利用角平分线的性质求出∠AOM,∠BON,即可求出∠MON;
④利用③的方法求出∠MON的度数;
(3)先求出∠BOC,利用角平分线的性质分别求出∠AOM,∠BON,再根据角度的关系求出答案即可.
(1)①∵![]() ,
,![]() ,
,
∴BC=AB-AC=4,
∵![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
∴![]() ,
, ![]() ,
,
∴MN=AB-AM-BN=6-1-2=3;
②∵![]() ,
,![]() ,
,
∴BC=AB-AC=a-b,
∵![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
∴![]() ,
,![]() ,
,
∴MN=AB-AM-BN=![]() =
=![]() ,
,
故答案为:![]() ;
;
(2)③∵![]() ,
,![]() ,
,
∴∠BOC=∠AOB-∠AOC=50![]() ,
,
∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴∠AOM=15![]() ,∠BON=25
,∠BON=25![]() ,
,
∴∠MON=∠AOB-∠AOM-∠BON=40![]() ;
;
④∵![]() ,
,![]() ,
,
∴∠BOC=(80-m)![]() ,
,
∵![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴∠AOM=![]() ,∠BON=(40-
,∠BON=(40-![]() m)
m)![]() ,
,
∴∠MON=∠AOB-∠AOM-∠BON=40![]() ,
,
故答案为:40;
(3)∵![]() ,
,![]() ,
,
∴∠BOC=∠AOC-∠AOB=(m-n)![]() ,
,
∵![]() 和
和![]() 的角平分线分别是
的角平分线分别是![]() ,
,![]() ,
,
∴∠AOM=![]() ,∠CON=
,∠CON=![]() ,
,
∴∠MON=∠AOC-∠AOM-∠CON=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内有两点E、F满足AE=1,EF=FC=3,AE⊥EF,CF⊥EF,则正方形ABCD的边长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,点P从B出发,沿折线BE-ED-DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则下列结论正确的有( )
①a=7 ②AB=8cm ③b=10 ④当t=10s时,y=12cm2

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在每个边长都为1的小正方形组成的网格中,点A、P分别为小正方形的中点,B为格点.
(I)线段AB的长度等于_____;
(Ⅱ)在线段AB上存在一个点Q,使得点Q满足∠PQA=45°,请你借助给定的网格,并利用不带刻度的直尺作出∠PQA,并简要说明你是怎么找到点Q的:_____.
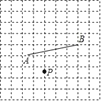
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 年
年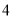 月
月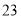 日是第
日是第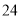 个世界读书日,为迎接第
个世界读书日,为迎接第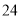 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;参赛者
推荐语
读书心得
读书讲座
甲
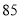
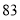
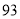
乙
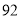
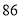
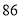
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按
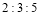 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由. -
科目: 来源: 题型:
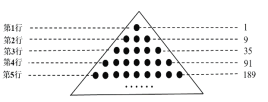
查看答案和解析>>【题目】如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右从小到大,且相邻两个点所表示的数相差1,每行数的和等于右边相应的数字,那么,表示2020的点在第______行,从左向右第______个位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的月历,图中带阴影的方框恰好盖住四个数,不改变带阴影的方框的形状大小,移动方框的位置.
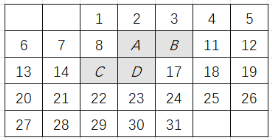
(1)若带阴影的方框盖住的4个数中,A表示的数是x,求这4个数的和(用含x的代数式表示);
(2)若带阴影的方框盖住的4个数之和为82,求出A表示的数;
(3)这4个数之和可能为38或112吗?如果可能,请求出这4个数,如果不可能,请说明理由.
相关试题

