【题目】已知,直线AB与直线CD相交于O,OB平分∠DOF.

(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(![]() ),求∠AOE的度数(用含x的代数式表示).
),求∠AOE的度数(用含x的代数式表示).
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 为
为![]() ;当
;当![]() 时,
时,![]() 为
为![]()
【解析】
(1)根据 OB平分∠DOF,可知∠BOD=∠BOF=40°,可求∠AOC的度数;
(2)①![]() 时分成两种情况:②
时分成两种情况:②![]() 时也分成两种情况.画出图形可求解.
时也分成两种情况.画出图形可求解.
解:(1)如图,
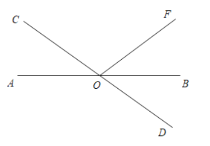
∵OB平分∠DOF
∴∠BOD=∠BOF=40°
又∵∠AOC与∠BOD互为对顶角
∴∠AOC=∠BOD=40°
∴∠AOC=40°
(2)①![]() 时分成两种情况:
时分成两种情况:
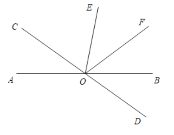
如上图情况:∠AOE=∠AOC+∠COE=x°+60°
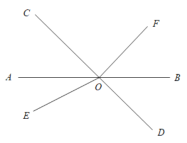
如上图情况:∠AOE=∠COE-∠AOC=60°-x°
②![]() 时也分成两种情况:
时也分成两种情况:
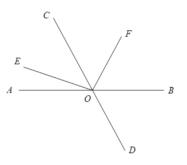
如上图情况:∠AOE=∠AOC-∠COE=x°-60°

如上图情况:∠AOE=∠AOC+∠COE=x°+60°
综上所述:当![]() 时,∠AOE为60°-x°或60°+x°
时,∠AOE为60°-x°或60°+x°
当![]() 时,∠AOE为x°-60°或60°+x°
时,∠AOE为x°-60°或60°+x°
-
科目: 来源: 题型:
查看答案和解析>>【题目】
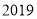 年
年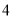 月
月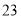 日是第
日是第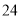 个世界读书日,为迎接第
个世界读书日,为迎接第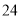 个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;
个世界读书日的到来,某校举办读书分享大赛活动:大赛以“推荐分享”为主题,参赛者选择一本自己最喜欢的书,然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座.大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分(各项成绩均按百分制),综合成绩排名第一的选手将获得大赛一等奖.现有甲、乙两位同学的各项成绩如下表所示;参赛者
推荐语
读书心得
读书讲座
甲
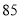
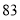
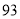
乙
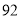
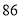
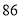
(1)若将三项成绩的平均分作为参赛选手的综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
(2)若“推荐语”“读书心得”“读书讲座”的成绩按
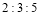 确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由.
确定综合成绩,则甲、乙二人谁最有可能获得大赛一等奖?请通过计算说明理由. -
科目: 来源: 题型:
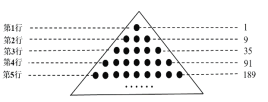
查看答案和解析>>【题目】如图,一个点表示一个数,不同位置的点表示不同的数,每行各点所表示的数自左向右从小到大,且相邻两个点所表示的数相差1,每行数的和等于右边相应的数字,那么,表示2020的点在第______行,从左向右第______个位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的月历,图中带阴影的方框恰好盖住四个数,不改变带阴影的方框的形状大小,移动方框的位置.
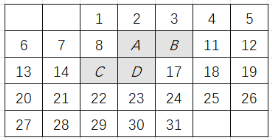
(1)若带阴影的方框盖住的4个数中,A表示的数是x,求这4个数的和(用含x的代数式表示);
(2)若带阴影的方框盖住的4个数之和为82,求出A表示的数;
(3)这4个数之和可能为38或112吗?如果可能,请求出这4个数,如果不可能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, ,
, ,点
,点 是
是 边上的中点,点
边上的中点,点 是
是 上的一动点(不与点
上的一动点(不与点 重合),延长
重合),延长 交射线
交射线 于点
于点 ,连结
,连结 、
、 .
.
 求证:四边形
求证:四边形 是平行四边形;
是平行四边形; 填空:①当
填空:①当 ________时,四边形
________时,四边形 是矩形;②当
是矩形;②当 ________时,四边形
________时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
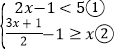
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教育局为了解本地八年级学生参加社会实践活动情况,随机抽查了部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)α= ,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该地共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
相关试题

