【题目】解不等式组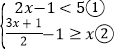
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
参考答案:
【答案】(I)x<3;(II)x≥1;(III)见解析;(IV)1≤x<3.
【解析】分析:(I)根据不等式的性质求出不等式的解集即可;
(II)根据不等式的性质求出不等式的解集即可;
(III)在数轴上表示出来即可;
(IV)根据数轴得出即可.
详解:(I)解不等式①得:x<3,
故答案为:x<3;
(II)解不等式②得:x≥1,
故答案为:x≥1;
(III)把不等式①和②的解集在数轴上表示出来为:
![]() ;
;
(IV)原不等式组的解集为1≤x<3,
故答案为:1≤x<3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )

A.(2017,0)
B.(2017 ,
, 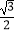 )
)
C.(2018, )
)
D.(2018,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)如图①,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB;


(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC,∠DCB=30°,求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
 ÷(a+2﹣
÷(a+2﹣  ),其中x2﹣2
),其中x2﹣2  x+a=0有两个不相等的实数根,且a为非负整数.
x+a=0有两个不相等的实数根,且a为非负整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
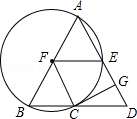
(1)求证:GC是⊙F的切线;
(2)填空: ①若∠BAD=45°,AB=2 ,则△CDG的面积为 .
,则△CDG的面积为 .
②当∠GCD的度数为时,四边形EFCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某居民区道路上的“早市”引起了大家关注,小明想了解本小区居民对“早市”的看法,进行了一次抽样调查,把居民对“早市”的看法分为四个层次:A、非常赞同B、赞同但要有一定的限制;C、无所谓D、不赞同,并将调查结果绘制了图1和图2两幅不完整的统计图.
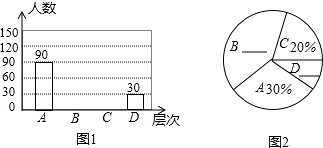
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“早市”的看法表示赞同(包括A层次).
相关试题

