【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.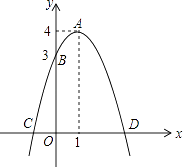
(1)求此抛物线的解析式;
(2)求C,D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD= ![]() S△BCD , 求点P的坐标.
S△BCD , 求点P的坐标.
参考答案:
【答案】
(1)
解:∵抛物线的顶点为A(1,4),
∴设抛物线的解析式y=a(x﹣1)2+4,
把点B(0,3)代入得,a+4=3,
解得a=﹣1,
∴抛物线的解析式为y=﹣(x﹣1)2+4
(2)
解:由(1)知,抛物线的解析式为y=﹣(x﹣1)2+4;
令y=0,则0=﹣(x﹣1)2+4,
∴x=﹣1或x=3,
∴C(﹣1,0),D(3,0);
∴CD=4,
∴S△BCD= ![]() CD×|yB|=
CD×|yB|= ![]() ×4×3=6
×4×3=6
(3)
解:由(2)知,S△BCD= ![]() CD×|yB|=
CD×|yB|= ![]() ×4×3=6;CD=4,
×4×3=6;CD=4,
∵S△PCD= ![]() S△BCD,
S△BCD,
∴S△PCD= ![]() CD×|yP|=
CD×|yP|= ![]() ×4×|yP|=3,
×4×|yP|=3,
∴|yP|= ![]() ,
,
∵点P在x轴上方的抛物线上,
∴yP>0,
∴yP= ![]() ,
,
∵抛物线的解析式为y=﹣(x﹣1)2+4;
∴ ![]() =﹣(x﹣1)2+4,
=﹣(x﹣1)2+4,
∴x=1± ![]() ,
,
∴P(1+ ![]() ,
, ![]() ),或P(1﹣
),或P(1﹣ ![]() ,
, ![]() )
)
【解析】(1)设抛物线顶点式解析式y=a(x﹣1)2+4,然后把点B的坐标代入求出a的值,即可得解;(2)令y=0,解方程得出点C,D坐标,再用三角形面积公式即可得出结论;(3)先根据面积关系求出点P的坐标,求出点P的纵坐标,代入抛物线解析式即可求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
x
…
﹣2
﹣1
0
1
2
…
y
…
﹣15.5
﹣5
﹣3.5
﹣2
﹣3.5
…
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70

英语
88
82
94
85
76
85
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A,B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .
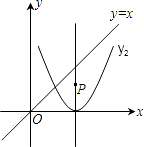
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1个单位长度,格点三角形(顶点是网络线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-1,3)
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的
 ;
;(3)直接写出点
 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.
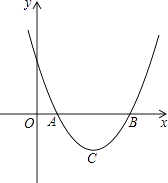
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值. -
科目: 来源: 题型:
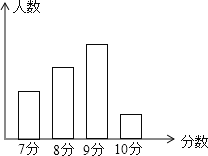
查看答案和解析>>【题目】体育课上,体育老师对七年级一个班的学生进行了立定跳远项目的测试,得到一组测试分数的数据,并将测试所得分数绘制如图所示的统计图,图中从左到右的学生数人数之比为2 : 3 : 4 : 1,且成绩为8分的学生有12人,根据以上信息解答下列问题:
(1) 这个班级有多少名学生?
(2)这组数据的众数是 分,中位数是 分.
(3)这个班级学生立定跳远项目测试的平均成绩是多少?
相关试题

