【题目】初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣15.5 | ﹣5 | ﹣3.5 | ﹣2 | ﹣3.5 | … |
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y= .
参考答案:
【答案】﹣5
【解析】解:∵点(0,﹣3.5)、(2,﹣3.5)在二次函数y=ax2+bx+c的图象上,
∴二次函数图象的对称轴为x= ![]() =1,
=1,
∵1×2﹣3=﹣1,且点(﹣1,﹣5)在二次函数y=ax2+bx+c的图象上,
∴当x=3时,二次函数y=ax2+bx+c中y=﹣5.
故答案为:﹣5.
由点的坐标结合二次函数的对称性可以找出该二次函数图象的对称轴,找出与x=3对称的点的坐标,由此即可得出y值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
(1)求证:△ABD≌△CAE;
(2)若∠FBA=60°,连结DF、EF,判断△DEF的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连结MN,作AH⊥MN,垂足为点H
(1)如图1,猜想AH与AB有什么数量关系?并证明;
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;
小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?

-
科目: 来源: 题型:
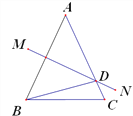
查看答案和解析>>【题目】如图,在△ABC,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A
B
C
D
E
平均分
标准差
数学
71
72
69
68
70

英语
88
82
94
85
76
85
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A,B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .
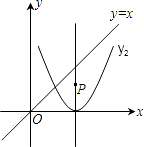
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
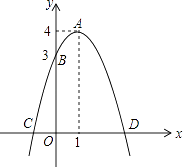
(1)求此抛物线的解析式;
(2)求C,D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD= S△BCD , 求点P的坐标.
S△BCD , 求点P的坐标.
相关试题

