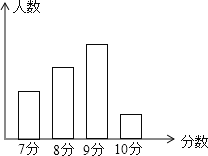
【题目】体育课上,体育老师对七年级一个班的学生进行了立定跳远项目的测试,得到一组测试分数的数据,并将测试所得分数绘制如图所示的统计图,图中从左到右的学生数人数之比为2 : 3 : 4 : 1,且成绩为8分的学生有12人,根据以上信息解答下列问题:
(1) 这个班级有多少名学生?
(2)这组数据的众数是 分,中位数是 分.
(3)这个班级学生立定跳远项目测试的平均成绩是多少?
参考答案:
【答案】(1)40人,(2)9;8.5;(3)8.4分.
【解析】
(1)根据得7分、8分、9分和10分的人数之比为2 : 3 : 4 : 1,且得8分的人数为12,即可求得该班的总人数;
(2)根据(1)中所求得的总人数即可求出得分分别为7分、9分和10分的人数,结合中位数和众数的定义即可确定出这组数据的中位数和众数;
(3)根据得分为7分、8分、9分和10分的人数即可求出该班这次立定跳远成绩的平均得分.
(1)∵立定跳远测试成绩得7分、8分、9分和10分的人数之比为2 : 3 : 4 : 1,且得分为8分的有12人,
∴ 该班的总人数为:12÷3×(2+3+4+1)=40(人);
(2)∵该班的总人数为40人,立定跳远测试成绩得7分、8分、9分和10分的人数之比为2 : 3 : 4 : 1,
∴得分为7分的人数=![]() ;
;
得分为9分的人数=![]() ;
;
得分为10分的人数=![]() ;
;
∵得分为8分的有12人,
∴该班立定跳远成绩的众数是9分,
∵将成绩按从小到大排列后,第20个和21个成绩分别为8分和9分,
∴该班立定跳远成绩的中位数是8.5分;
(3)由(2)可得,该班立定跳远成绩的平均分为:
![]() (分).
(分).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
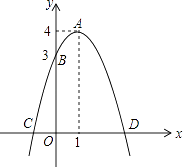
(1)求此抛物线的解析式;
(2)求C,D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD= S△BCD , 求点P的坐标.
S△BCD , 求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1个单位长度,格点三角形(顶点是网络线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-1,3)
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的
 ;
;(3)直接写出点
 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.
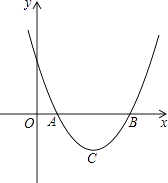
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中, 直角三角形的个数为
①
 ②
②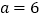 ,∠A=45°;③∠A=32°, ∠B=58°;
,∠A=45°;③∠A=32°, ∠B=58°;④
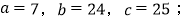 ⑤
⑤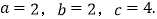 ⑥
⑥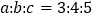
⑦
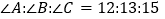 ⑹
⑹
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
求证:DB=DC.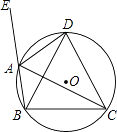
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级同学到距学校6km的郊外游玩,一部分同学步行,另一部分同学骑车。如图,
 分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用的时间x(min)之间的函数图像,则下列判断错误的是
分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用的时间x(min)之间的函数图像,则下列判断错误的是 
A. 骑车的同学比步行的同学晚出发30min
B. 步行的同学的速度是6km/h
C. 骑车的同学从出发到追上步行的同学用了20min
D. 骑车的同学和步行的同学同时到达目的地
相关试题

