【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

参考答案:
【答案】(1)90°,直径所对的圆周角是直角;
(2)△EAD是等腰三角形,理由见解析;
(3)BD=![]()
【解析】试题分析:(1)根据AB是⊙O的直径,点C在⊙O上利用直径所对的圆周角是直角即可得到结论;
(2)根据∠ABC的平分线与AC相交于点D,得到∠CBD=∠ABE,再根据AE是⊙O的切线得到∠EAB=90°,从而得到∠CDB+∠CBD=90°,等量代换得到∠AED=∠EDA,从而判定△EAD是等腰三角形.
(3)证得△CDB∽△AEB后设BD=5x,则CB=4x,CD=3x,从而得到CA=CD+DA=3x+6,然后在直角三角形ACB中,利用AC2+BC2=AB2得到(3x+6)2+(4x)2=82解得x后即可求得BD的长.
试题解析:(1)∵AB是⊙O的直径,点C在⊙O上,
∴∠ACB=90°(直径所对的圆周角是直角)
(2)△EAD是等腰三角形.
证明:∵∠ABC的平分线与AC相交于点D,
∴∠CBD=∠ABE
∵AE是⊙O的切线,∴∠EAB=90°
∴∠AEB+∠EBA=90°,
∵∠EDA=∠CDB,∠CDB+∠CBD=90°,
∵∠CBE=∠ABE,
∴∠AED=∠EDA,
∴AE=AD
∴△EAD是等腰三角形.
(3)解:∵AE=AD,AD=6,
∴AE=AD=6,
∵AB=8,
∴在直角三角形AEB中,EB=10
∵∠CDB=∠E,∠CBD=∠ABE
∴△CDB∽△AEB,
∴![]() ,
,
∴设CB=4x,CD=3x则BD=5x,
∴CA=CD+DA=3x+6,
在直角三角形ACB中,
AC2+BC2=AB2
即:(3x+6)2+(4x)2=82,
解得:x=﹣2(舍去)或x=![]()
∴BD=5x=![]() .
.
-
科目: 来源: 题型:
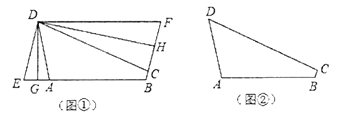
查看答案和解析>>【题目】定义:有三个角相等的四边形叫做三等角四边形.
(1)在三等角四边形
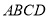 中,
中,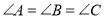 ,则
,则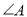 的取值范围为________.
的取值范围为________.(2)如图①,折叠平行四边形
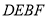 ,使得顶点
,使得顶点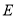 、
、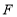 分别落在边
分别落在边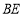 、
、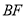 上的点
上的点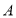 、
、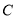 处,折痕为
处,折痕为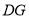 、
、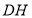 .求证:四边形
.求证:四边形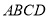 为三等角四边形;
为三等角四边形;(3)如图②,三等角四边形
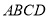 中,
中,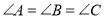 ,若
,若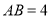 ,
,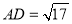 ,
,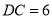 ,则
,则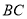 的长度为多少?
的长度为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,
 ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (
 ,
, ) B. (
) B. ( ,
, ) C. (
) C. ( ,
, ) D. (
) D. ( ,4
,4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )条

A.3条B.4条C.6条D.12条
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,仅用直尺和圆规画一个长方形,使它的面积是图中长方形面积的4倍.
(2)若新的长方形的长与宽的比为4:3,且周长为56厘米,求新长方形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a的方程
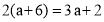 的解也是关于x的方程
的解也是关于x的方程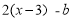 =11的解.
=11的解.(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使
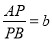 ,点Q为AP的中点,求线段BQ的长.
,点Q为AP的中点,求线段BQ的长. -
科目: 来源: 题型:
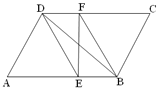
查看答案和解析>>【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
相关试题

