【题目】已知关于a的方程![]() 的解也是关于x的方程
的解也是关于x的方程![]() =11的解.
=11的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() ,点Q为AP的中点,求线段BQ的长.
,点Q为AP的中点,求线段BQ的长.
参考答案:
【答案】(1)a=10,b=3;(2)![]() 或
或![]() .
.
【解析】
(1)根据方程同解,求出第一个方程的解,可求出第二个方程中的b;
(2)分类讨论,①点P在线段AB上,根据![]() ,可求出PB的长,根据Q是线段PB的中点,可求出BQ的长;②点P在线段AB的延长线上,根据
,可求出PB的长,根据Q是线段PB的中点,可求出BQ的长;②点P在线段AB的延长线上,根据![]() ,可求出PB的长,根据Q是线段PB的中点,可得BQ的长.
,可求出PB的长,根据Q是线段PB的中点,可得BQ的长.
解:![]()
![]()
![]()
![]()
∵x=a=10,
把x=10代入![]() 得:
得:![]() ,解得:b=3;
,解得:b=3;
(2)①当点P在线段AB上时,如图所示:
![]()
∴AB=a=10,![]() ,
,
∴AP=3PB,则AB=AP+PB=4PB=10,
∴PB=2.5,
∵Q是线段PB的中点,
∴![]() ;
;
②当点P在线段AB延长线上时,如图所示:
![]()
∴AB=a=10,![]() ,
,
∴AP=3PB,AB=AP-PB=2PB=10,
∴PB=5,
∵Q是线段PB的中点,
∴![]() ,
,
综上所述:BQ的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )条

A.3条B.4条C.6条D.12条
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,仅用直尺和圆规画一个长方形,使它的面积是图中长方形面积的4倍.
(2)若新的长方形的长与宽的比为4:3,且周长为56厘米,求新长方形的面积.

-
科目: 来源: 题型:
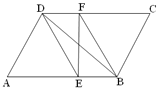
查看答案和解析>>【题目】已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某购物网站上一种小礼品按销售量分三部分制定阶梯销售单价,如下表:
销售量
单价
不超过120件的部分
3.5元/件
超过120件不超过300件的部分
3.2元/件
超过300件的部分
3.0元/件
(1)“双十一”期间,购物总金额累计满300元可使用50元购物津贴(即累计总金额每满300减50元),若购买85件,花费 元;若购买120件,花费 元;若购买250件,花费 元.
(2)“双十一”期间,王老师购买这种小礼品花了335元,列方程求王老师购买了这种小礼品多少件?
(3)“双十二”即将来临,但“双十二”期间不能使用购物津贴,王老师和李老师各自单独购买这种小礼品共400件,其中王老师的购买数量大于李老师的购买数量,她们一共花费1336元,请问王老师和李老师各购买这种小礼品多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
相关试题

