【题目】定义:有三个角相等的四边形叫做三等角四边形.
(1)在三等角四边形![]() 中,
中,![]() ,则
,则![]() 的取值范围为________.
的取值范围为________.
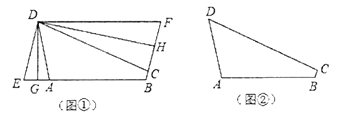
(2)如图①,折叠平行四边形![]() ,使得顶点
,使得顶点![]() 、
、![]() 分别落在边
分别落在边![]() 、
、![]() 上的点
上的点![]() 、
、![]() 处,折痕为
处,折痕为![]() 、
、![]() .求证:四边形
.求证:四边形![]() 为三等角四边形;
为三等角四边形;
(3)如图②,三等角四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长度为多少?
的长度为多少?
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的长度为
的长度为![]() .
.
【解析】
(1)根据四边形的内角和是360°,确定出∠BAD的范围;
(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC即可;
(3)延长BA,过D点作DG⊥BA,继续延长BA,使得AG=EG,连接DE;延长BC,过D点作DH⊥BC,继续延长BC,使得CH=HF,连接DF,由SAS证明△DEG≌△DAG,得出AD=DE=![]() ,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=6,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=6,DE=BF=
,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=6,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=6,DE=BF=![]() ,由等腰三角形的性质得出EG=AG=
,由等腰三角形的性质得出EG=AG=![]() (BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=
(BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=![]() =4,由平行四边形DEBF的面积求出
=4,由平行四边形DEBF的面积求出![]() ,在Rt△DCH中,由勾股定理求出
,在Rt△DCH中,由勾股定理求出![]() ,即可得出BC的长度.
,即可得出BC的长度.
(1)∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
故答案为:![]()
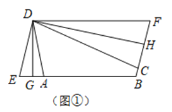
(2)证明:∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴四边形![]() 是三等角四边形;
是三等角四边形;
(3)延长![]() ,过
,过![]() 点作
点作![]() ,继续延长
,继续延长![]() ,使得
,使得![]() ,连接
,连接![]() ;延长
;延长![]() ,过
,过![]() 点作
点作![]() ,继续延长
,继续延长![]() ,使得
,使得![]() ,连接
,连接![]() ,如图所示:
,如图所示:
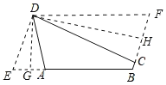
在![]() 和
和![]() 中,
中,
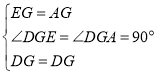
∴![]()
![]() ,
,
∴![]() ,
,![]()
同理可得![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]()
在![]() 中,
中,![]()
∵平行四边形![]() 的面积
的面积![]() ,
,
即:![]()
∴![]()
在![]() 中,
中,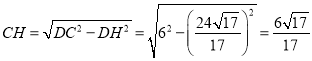
∴![]()
故答案为:![]() 的长度为
的长度为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计,绘制了两幅尚不完整的统计图如图所示,
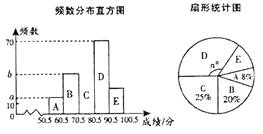
根据统计图中的信息解答下列问题:
(1)若
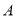 组的频数比
组的频数比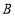 组小
组小 ,则频数分布直方图中
,则频数分布直方图中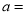 ________,
________,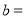 ________;
________;(2)扇形统计图中
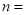 ________,并补全频数分布直方图;
________,并补全频数分布直方图;(3)若成绩在
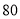 分以上为优秀,全校共有
分以上为优秀,全校共有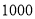 名学生,请估计成绩优秀的学生有多少名?
名学生,请估计成绩优秀的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了
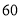 次实验,实验的结果如下:
次实验,实验的结果如下:朝上的点数
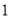
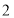
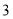
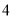
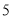
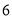
出现的次数
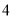
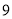
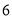
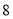
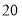
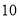
(1)计算“
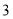 点朝上”的频率和“
点朝上”的频率和“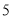 点朝上”的频率.
点朝上”的频率.(2)小颖说:“根据实验得出,出现
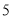 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷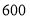 次,那么出现
次,那么出现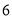 点朝上的次数正好是
点朝上的次数正好是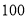 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,
 ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (
 ,
, ) B. (
) B. ( ,
, ) C. (
) C. ( ,
, ) D. (
) D. ( ,4
,4 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )条

A.3条B.4条C.6条D.12条
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

相关试题

