【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )

A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,4
,4![]() )
)
参考答案:
【答案】C
【解析】试题分析:利用等面积法求O'的纵坐标,再利用勾股定理或三角函数求其横坐标:
如答图,过O’作O’F⊥x轴于点F,过A作AE⊥x轴于点E,
∵A的坐标为(2,![]() ),∴AE=
),∴AE=![]() ,OE=2.
,OE=2.
由等腰三角形底边上的三线合一得OB=2OE=4,
在Rt△ABE中,由勾股定理可求AB=3,则A’B=3,
由旋转前后三角形面积相等得![]() ,即
,即![]() ,
,
∴O’F=![]() ·
·
在Rt△O’FB中,由勾股定理可求BF=![]() ,∴OF=
,∴OF=![]() .
.
∴O’的坐标为(![]() ).
).
故选C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了加强学生的安全意识,组织学生参加安全知识竞赛,并从中抽取了部分学生的成绩(得分均为整数,满分100分)进行统计,绘制了两幅尚不完整的统计图如图所示,
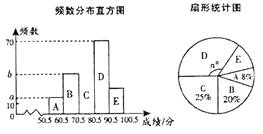
根据统计图中的信息解答下列问题:
(1)若
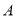 组的频数比
组的频数比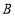 组小
组小 ,则频数分布直方图中
,则频数分布直方图中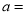 ________,
________,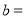 ________;
________;(2)扇形统计图中
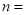 ________,并补全频数分布直方图;
________,并补全频数分布直方图;(3)若成绩在
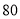 分以上为优秀,全校共有
分以上为优秀,全校共有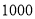 名学生,请估计成绩优秀的学生有多少名?
名学生,请估计成绩优秀的学生有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在做投掷骰子(质地均匀的正方体)实验,他们共做了
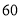 次实验,实验的结果如下:
次实验,实验的结果如下:朝上的点数
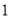
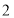
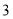
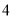
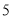
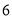
出现的次数
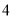
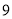
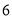
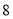
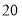
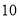
(1)计算“
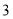 点朝上”的频率和“
点朝上”的频率和“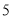 点朝上”的频率.
点朝上”的频率.(2)小颖说:“根据实验得出,出现
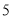 点朝上的机会最大”;小红说:“如投掷
点朝上的机会最大”;小红说:“如投掷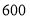 次,那么出现
次,那么出现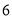 点朝上的次数正好是
点朝上的次数正好是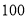 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有三个角相等的四边形叫做三等角四边形.
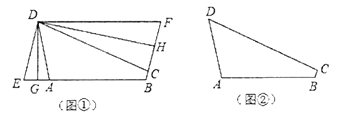
(1)在三等角四边形
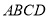 中,
中,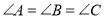 ,则
,则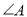 的取值范围为________.
的取值范围为________.(2)如图①,折叠平行四边形
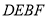 ,使得顶点
,使得顶点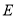 、
、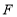 分别落在边
分别落在边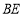 、
、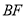 上的点
上的点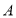 、
、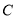 处,折痕为
处,折痕为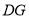 、
、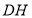 .求证:四边形
.求证:四边形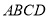 为三等角四边形;
为三等角四边形;(3)如图②,三等角四边形
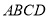 中,
中,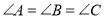 ,若
,若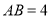 ,
,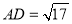 ,
,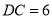 ,则
,则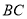 的长度为多少?
的长度为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )条

A.3条B.4条C.6条D.12条
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在⊙O上,∠ABC的平分线与AC相交于点D,与⊙O过点A的切线相交于点E.
(1)∠ACB= °,理由是: ;
(2)猜想△EAD的形状,并证明你的猜想;
(3)若AB=8,AD=6,求BD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,仅用直尺和圆规画一个长方形,使它的面积是图中长方形面积的4倍.
(2)若新的长方形的长与宽的比为4:3,且周长为56厘米,求新长方形的面积.

相关试题

