搜索
【题目】已知：如图，等边三角形ABC中，D、E分别是BC、AC上的点，且AE=CD，
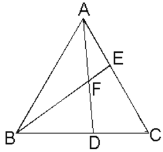
（1）求证：AD=BE
（2）求：∠BFD的度数.
参考答案：
【答案】（1）见解析；（2）60°.
【解析】
（1）根据等边三角形各边长相等的性质可得AB=AC，易证△ABE≌△CAD可得AD=BE；
（2）根据全等三角形对应角相等可得∠ABE=∠CAD，进而根据∠BFD=∠BAD+∠ABE即可求∠BFD的度数．
(1)证明：∵△ABC是等边三角形，
∴∠BAC=∠C=60°，AB=CA，
在△ABE和△CAD中
，
∴△ABE≌△CAD(SAS)，
∴AD=BE(全等三角形对应边相等)；
(2)∵△ABE≌△CAD(已证)，
∴∠ABE=∠CAD(全等三角形对应角相等)，
又∵∠BFD=∠BAD+∠ABE，
∴∠BFD=∠BAD+∠CAD=∠BAC，
又∠BAC=60°，
∴∠BFD=60°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的三个顶点分别为
， 
， 
.若反比例函数
在第一象限内的图象与△ABC有公共点，则k的取值范围是__________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在Rt△ABC中，∠C=90°，AC=BC=2，点D、E分别在边AC、AB上，AD=DE=
AB，连接DE．将△ADE绕点A逆时针方向旋转，记旋转角为θ．（1）问题发现
①当θ=0°时，
= ；②当θ=180°时，
= ．（2）拓展探究
试判断：当0°≤θ＜360°时，
的大小有无变化？请仅就图2的情形给出证明；（3）问题解决
①在旋转过程中，BE的最大值为 ；
②当△ADE旋转至B、D、E三点共线时，线段CD的长为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A点坐标为(5，0)，直线y＝kx+b(b＞0)与y轴交于点B，∠BCA＝60°，连接AB，∠α＝105°，则直线y＝kx+b的表达式为( )
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】线段AB的两端点的坐标为A(﹣1，0)，B(0，﹣2)．现请你在坐标轴上找一点P，使得以P、A、B为顶点的三角形是直角三角形，则满足条件的P点的坐标是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线y＝－x＋1与抛物线y＝ax2＋bx＋c(a≠0)相交于点A(1，0)和点D(－4，5)，并与y轴交于点C，抛物线的对称轴为直线x＝－1，且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式；
(2)若点E是直线下方抛物线上的一个动点，求出△ACE面积的最大值；
(3)如图2，若点M是直线x＝－1的一点，点N在抛物线上，以点A，D，M，N为顶点的四边形能否成为平行四边形？若能，请直接写出点M的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，点D、E分别是斜边AB和直角边BC上的点，把△ABC沿着直线DE折叠，顶点B的对应点是点B′．
(1)如图①，如果点B′和点A重合，求CE的长．
(2)如图②，如果点B′落在直角边AC的中点上，求BE的长．
相关试题
