【题目】如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
根据等腰直角三角形的性质和三角函数分别求B、C两点的坐标,利用待定系数法求直线的表达式.
∵A点坐标为(5,0),
∴OA=5,
∵∠BCA=60°,∠α=105°,
∴∠BAC=105°﹣60°=45°,
∴△AOB是等腰直角三角形,
∴AO=BO=5,
∴B(0,5).
∵∠CBO=90°﹣∠BCA=30°,
∴BC=2CO,BO=![]() =
=![]() CO=5,
CO=5,
∴CO=![]() ,
,
∴C(﹣![]() ,0),
,0),
把B(0,5)和C(﹣![]() ,0)代入y=kx+b中得:
,0)代入y=kx+b中得: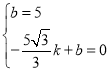 ,
,
解得: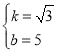 ,
,
∴直线BC的表达式为:y=![]() x+5.
x+5.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(﹣
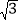 ,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( ) 
A.
 B.
B.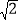 C.
C. D.2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点分别为
 ,
,  ,
,  .若反比例函数
.若反比例函数 在第一象限内的图象与△ABC有公共点,则k的取值范围是__________.
在第一象限内的图象与△ABC有公共点,则k的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=
 AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.(1)问题发现
①当θ=0°时,
 = ;
= ;②当θ=180°时,
 = .
= .(2)拓展探究
试判断:当0°≤θ<360°时,
 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD,
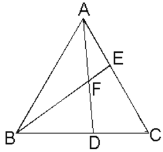
(1)求证:AD=BE
(2)求:∠BFD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB的两端点的坐标为A(﹣1,0),B(0,﹣2).现请你在坐标轴上找一点P,使得以P、A、B为顶点的三角形是直角三角形,则满足条件的P点的坐标是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线y=-x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(-4,5),并与y轴交于点C,抛物线的对称轴为直线x=-1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=-1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.

相关试题

