【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
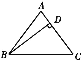
(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
参考答案:
【答案】(1)证明见解析;(2)△ABC的面积为75.
【解析】
(1)由勾股定理逆定理可以证明△BCD是直角三角形;(2)要求△BCD的面积,已知BD的长度,即要求AC的长度,已知CD的长度,即要求AD的长度,设AD=x,根据勾股定理列方程求解.
(1)证明:∵ CD=9,BD=12,
∴ CD2+BD2=92+122=225,
∵ BC=15,∴ BC2=225,
∴ CD2+BD2=BC2,
∴ △BCD是直角三角形,且∠BDC=90°;
(2)设AD=x,则AC=x+9,
∵ AB=AC,∴ AB=x+9,
∵ ∠BDC=90°,∴ ∠ADB=90°,
∴ AB2=AD2+BD2,
∴ ![]() ,
,
解得:x=![]() ,
,
∴AC=![]() +9=
+9=![]() ,
,
∴S△ABC=![]() AC×BD=
AC×BD=![]() ×
×![]() ×12=75,
×12=75,
∴ △ABC的面积为75.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.

(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.
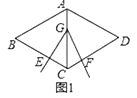
(1)如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;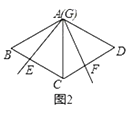
(2)知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
②在顶点G的运动过程中,若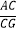 =t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
=t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);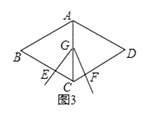
(3)问题解决:如图4,已知菱形边长为8,BG=7,CF=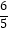 ,当t>2时,求EC的长度.
,当t>2时,求EC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).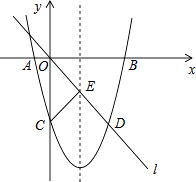
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形. -
科目: 来源: 题型:
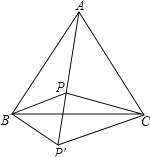
查看答案和解析>>【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程 (m3)xm27x+3=0 是关于x的一元二次方程,则方程( )
A.无实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.有一个根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
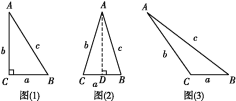
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
相关试题

