Question

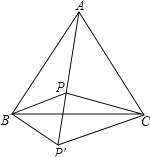
【题目】P为等边△ABC内的一点，PA=10，PB=6，PC=8，将△ABP绕点B顺时针旋转60°到△CBP′位置．

（1）判断△BPP′的形状，并说明理由；

（2）求∠BPC的度数．

Answer 1

【答案】(1) △BPP′是等边三角形，理由详见解析；(2)150°．

【解析】

试题分析：（1）根据旋转的性质得BP=BP′，∠PBP’=60°，AP=CP′=10，则利用等边三角形的判定方法可判断△BPP′是等边三角形；

（2）利用△BPP′是等边三角形得到∠BPP′=60°，PP′=PB=6，然后利用勾股定理的逆定理可证明△PCP′是直角三角形，∠P′PC=90°，再计算∠BPP′+∠P′PC即可．

试题解析：（1）△BPP′是等边三角形；理由如下：

∵△ABP绕点B顺时针旋转60°到△CBP′位置，

∴BP=BP′，∠PBP′=60°，AP=CP′=10，

∴△BPP′是等边三角形；

（2）∵△BPP′是等边三角形，

∴∠BPP′=60°，PP′=PB=6，

∵，

∴，

∴△PCP′是直角三角形，∠P′PC=90°，

∴∠BPC=∠BPP′+∠P′PC=60°+90°=150°．