【题目】若方程 (m3)xm27x+3=0 是关于x的一元二次方程,则方程( )
A.无实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.有一个根
参考答案:
【答案】C
【解析】∵方程 (m3)xm27x+3=0 是关于x的一元二次方程,
∴![]() ,
,
∴m=-3,
∴-6x2-x+3=0,
即:6x2+x-3=0,
∴△=12-4×6×(-3)=73![]() 0,
0,
∴方程有两个不相等的实数根.
所以答案是:C.
【考点精析】通过灵活运用一元二次方程的定义和求根公式,掌握只有一个未知数,并且未知数的项的最高系数为2的方程为一元二次方程;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(﹣2,0),(6,﹣8).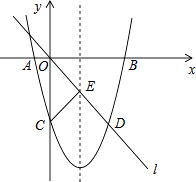
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q,试探究:当m为何值时,△OPQ是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
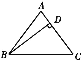
(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
-
科目: 来源: 题型:
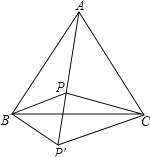
查看答案和解析>>【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
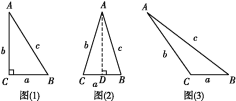
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别
A
B
C
D
处理方式
迅速离开
马上救助
视情况而定
只看热闹
人数
m
30
n
5
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
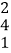
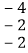
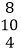
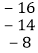
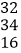
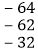
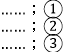
如图,在上面的数据中,用一个长方形圈出同一列的三个数,这列的第一个数表示为
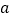 ,其余各数分别用a、
,其余各数分别用a、 表示:
表示: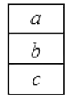
(1)若这三个数分别在这三行数的第
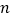 列,请用含
列,请用含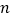 的式子分别表示
的式子分别表示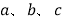 的值;
的值;(2)若
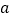 记为
记为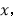 求
求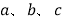 这三个数的和(结果用含
这三个数的和(结果用含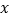 的式子表示并化简).
的式子表示并化简).
相关试题

