Question

【题目】如图，已知tan∠EOF=2，点C在射线OF上，OC=12．点M是∠EOF内一点，MC⊥OF于点C，MC=4．在射线CF上取一点A，连结AM并延长交射线OE于点B，作BD⊥OF于点D．

（1）当AC的长度为多少时，△AMC和△BOD相似；
（2）当点M恰好是线段AB中点时，试判断△AOB的形状，并说明理由；
（3）连结BC．当S△AMC=S△BOC时，求AC的长．

Answer 1

【答案】
（1）解：∵∠MCA=∠BDO=Rt∠，

∴△AMC和△BOD中，C与D是对应点，

∴△AMC和△BOD相似时分两种情况：

①当△AMC∽△BOD时， =tan∠EOF=2，

∵MC=4，

∴ =2，

解得AC=8；

②当△AMC∽△OBD时， =tan∠EOF=2，

∵MC=4，

∴ =2，

解得AC=2．

故当AC的长度为2或8时，△AMC和△BOD相似

（2）解：△ABO为直角三角形．理由如下：

∵MC∥BD，

∴△AMC∽△ABD，

∴ ，∠AMC=∠ABD，

∵M为AB中点，

∴C为AD中点，BD=2MC=8．

∵tan∠EOF=2，

∴OD=4，

∴CD=OC﹣OD=8，

∴AC=CD=8．

在△AMC与△BOD中，

，

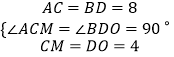∴△AMC≌△BOD（SAS），

∴∠CAM=∠DBO，

∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°，

∴△ABO为直角三角形

（3）解：连结BC，

设OD=a，则BD=2a．

∵S△AMC=S△BOC，S△AMC= AC MC=2AC，S△BOC= OC BD=12a，

∴2AC=12a，

∴AC=6a．

∵△AMC∽△ABD，

∴ ，即 ，

解得a1=3，a2=﹣ （舍去），

∴AC=6×3=18．

【解析】（1）△AMC和△BOD相似时分两种情况：△AMC∽△BOD和△AMC∽△OBD，再由相似三角形的对应边成比例求出AC的长；
（2）易证△AMC∽△ABD，根据相似三角形的性质和三角形的中位线性质可求出OD=4，CD=8，AC=CD=8，从而得出△AMC≌△BOD，则∠CAM=∠DBO，再由∠ABO=∠ABD+∠DBO=∠AMC+∠CAM可求出∠ABO的度数，进而得出△ABO的形状；
（3）设OD=a，则BD=2a．利用三角形的面积可得AC=6a，再由△AMC∽△ABD，根据相似三角形的对应边成比例可求出a的值，进而得出AC的长.