【题目】如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
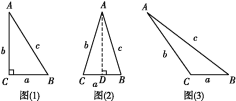
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
参考答案:
【答案】(1)a2+b2<c2;(2)证明见解析.
【解析】
(1)根据题意可猜测:当△ABC为钝角三角形时,a2+b2与c2的大小关系为:a2+b2<c2;
(2)过点A作AD⊥BC于点D;然后设CD=x,分别在Rt△ADC与Rt△ADB中,表示出AD2,即可证得结论.
(1)当△ABC为钝角三角形时,a2+b2与c2的大小关系为:a2+b2<c2;
(2)如图3,过点A作AD⊥BC于点D,设CD=x.
在Rt△ADC中,AD2=b2﹣x2.在Rt△ADB中,AD2=c2﹣(a+x)2,∴b2﹣x2=c2﹣(a+x)2,∴a2+b2=c2﹣2ax.
∵a>0,x>0,∴2ax>0,∴a2+b2<c2,∴当△ABC为钝角三角形时,a2+b2<c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
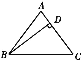
(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
-
科目: 来源: 题型:
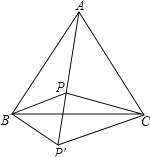
查看答案和解析>>【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程 (m3)xm27x+3=0 是关于x的一元二次方程,则方程( )
A.无实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.有一个根 -
科目: 来源: 题型:
查看答案和解析>>【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别
A
B
C
D
处理方式
迅速离开
马上救助
视情况而定
只看热闹
人数
m
30
n
5
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数:
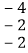
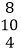
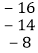
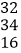
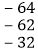
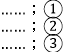
如图,在上面的数据中,用一个长方形圈出同一列的三个数,这列的第一个数表示为
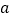 ,其余各数分别用a、
,其余各数分别用a、 表示:
表示: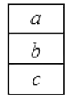
(1)若这三个数分别在这三行数的第
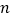 列,请用含
列,请用含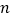 的式子分别表示
的式子分别表示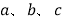 的值;
的值;(2)若
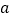 记为
记为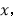 求
求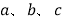 这三个数的和(结果用含
这三个数的和(结果用含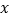 的式子表示并化简).
的式子表示并化简). -
科目: 来源: 题型:
查看答案和解析>>【题目】某年级共有330名男生,为了解该年级男生1000米跑步成绩(单位:分/秒)的情况,从中随机抽取30名男生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a.1000米跑步的频数分布表如下:
分组
3′17″<x≤3′ 37″
3′37″<x≤3′ 57″
3′ 57″<x≤4′ 17″
4′ 17″<x≤4′ 37″
4′ 37″<x≤4′ 57″
4′ 57″<x≤5′ 17″
频数
10
9
m
2
2
1
注:3′37″即3分37秒
b.1000米跑步在3′37″<x≤3′57″这一组是:
3′39 ″ 3′42 ″ 3′45 ″ 3′45″ 3′50 ″ 3′52 ″ 3′53″ 3′55″ 3′57″
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)根据表频数分布表画出相应的频数分布直方图.
(3)若男生1000米跑步成绩等于或者优于3′52″,成绩记为优秀.请估计全年级男生跑步成绩达到优秀的人数.
相关试题

