【题目】已知函数 ![]() .(a为常数,a>0) (Ⅰ)若
.(a为常数,a>0) (Ⅰ)若 ![]() 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;
(Ⅱ)求证:当0<a≤2时,f(x)在 ![]() 上是增函数;
上是增函数;
(Ⅲ)若对任意的a∈(1,2),总存在 ![]() ,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
参考答案:
【答案】由题得: 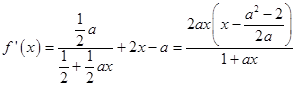 . (Ⅰ)由已知,得
. (Ⅰ)由已知,得 ![]() 且
且 ![]() ,∴a2﹣a﹣2=0,∵a>0,∴a=2
,∴a2﹣a﹣2=0,∵a>0,∴a=2
经检验:a=2符合题意.(2分)
(Ⅱ)当0<a≤2时,∵ ![]() ,∴
,∴ ![]() ,
,
∴当 ![]() 时,
时, ![]() .又
.又 ![]() ,
,
∴f'(x)≥0,故f(x)在 ![]() 上是增函数.
上是增函数.
(Ⅲ)a∈(1,2)时,由(Ⅱ)知,f(x)在 ![]() 上的最大值为
上的最大值为 ![]() ,
,
于是问题等价于:对任意的a∈(1,2),不等式 ![]() 恒成立.
恒成立.
记 ![]() ,(1<a<2)
,(1<a<2)
则 ![]() ,
,
当m=0时, ![]() ,∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,
,∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,
由于a2﹣1>0,∴m≤0时不可能使g(a)>0恒成立,
故必有m>0,∴ ![]() .
.
若 ![]() ,可知g(a)在区间
,可知g(a)在区间 ![]() 上递减,在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,故
上递减,在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,故 ![]() ,
,
这时,g'(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴ 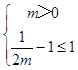 ,即
,即 ![]() ,
,
所以,实数m的取值范围为 ![]() .
.
【解析】(Ⅰ)先求出其导函数: 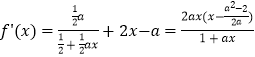 ,利用
,利用 ![]() 是函数f(x)的一个极值点对应的结论f'(
是函数f(x)的一个极值点对应的结论f'( ![]() )=0即可求a的值;(Ⅱ)利用:
)=0即可求a的值;(Ⅱ)利用: 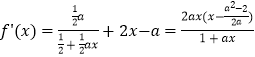 ,在0<a≤2时,分析出因式中的每一项都大于等于0即可证明结论;(Ⅲ)先由(Ⅱ)知,f(x)在
,在0<a≤2时,分析出因式中的每一项都大于等于0即可证明结论;(Ⅲ)先由(Ⅱ)知,f(x)在 ![]() 上的最大值为
上的最大值为 ![]() ,把问题转化为对任意的a∈(1,2),不等式
,把问题转化为对任意的a∈(1,2),不等式 ![]() 恒成立;然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数m的取值范围.
恒成立;然后再利用导函数研究不等式左边的最小值看是否符合要求即可求实数m的取值范围.
【考点精析】关于本题考查的函数的极值与导数,需要了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.

(1)求证:BC⊥D1E;
(2)若平面BCC1B1与平面BED1所成的锐二面角的大小为 ,求线段D1E的长度.
,求线段D1E的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
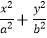 =1(a>b>0)的左焦点F1(﹣
=1(a>b>0)的左焦点F1(﹣ 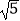 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
(1)求椭圆E的方程;
(2)过坐标原点O的直线交椭圆W: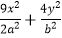 =1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB.
=1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的极坐标方程为ρsin(θ+
 )=
)=  ,圆C的参数方程为:
,圆C的参数方程为:  (其中θ为参数).
(其中θ为参数).
(1)判断直线l与圆C的位置关系;
(2)若椭圆的参数方程为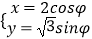 (φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
(φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣a|+a.
(1)若不等式f(x)≤6的解集为{x|﹣2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m﹣f(﹣n)成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】把函数f(x)=
 cos2x﹣sin2x的图象向右平移
cos2x﹣sin2x的图象向右平移  个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
A.[﹣ ,0]
,0]
B.[﹣π,0]
C.[﹣ ,
,  ]
]
D.[0, ]
]
相关试题

