【题目】已知直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() ,圆C的参数方程为:
,圆C的参数方程为: ![]() (其中θ为参数).
(其中θ为参数).
(1)判断直线l与圆C的位置关系;
(2)若椭圆的参数方程为 ![]() (φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
(φ为参数),过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A,B两点,求|AB|.
参考答案:
【答案】
(1)解:将直线l的极坐标方程 ![]() ,化为直角坐标方程:x+y﹣1=0.
,化为直角坐标方程:x+y﹣1=0.
将圆C的参数方程化为普通方程:x2+(y+2)2=4,圆心为C(0,﹣2),半径r=2.
∴圆心C到直线l的距离为d= ![]() >r=2,
>r=2,
∴直线l与圆C相离.
(2)解:将椭圆的参数方程化为普通方程为 ![]() ,
,
∵直线l:x+y﹣1=0的斜率为k1=﹣1,
∴直线l'的斜率为k2=1,即倾斜角为 ![]() ,
,
则直线l'的参数方程为 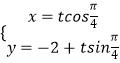 ,(t为参数),
,(t为参数),
即 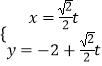 (t为参数),
(t为参数),
把直线l'的参数方程 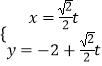 代入
代入 ![]() ,
,
整理得7t2﹣16 ![]() t+8=0.(*)
t+8=0.(*)
由于△=(﹣16 ![]() )2﹣4×7×8>0,
)2﹣4×7×8>0,
故可设t1,t2是方程(*)的两个不等实根,则有t1t2= ![]() ,
, ![]() ,
,
|AB|= ![]()
【解析】(1)将直线l的极坐标方程化为直角坐标方程,将圆C的参数方程化为普通方程,求出圆心C到直线l的距离,由此得到直线l与圆C相离.(2)将椭圆的参数方程化为普通方程为 ![]() ,求出直线l'的参数方程,把直线l'的参数方程代入椭圆的普通方程,得7t2﹣16
,求出直线l'的参数方程,把直线l'的参数方程代入椭圆的普通方程,得7t2﹣16 ![]() t+8=0,由此利用根的判别式、韦达定理、弦长公式能求出|AB|.
t+8=0,由此利用根的判别式、韦达定理、弦长公式能求出|AB|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
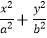 =1(a>b>0)的左焦点F1(﹣
=1(a>b>0)的左焦点F1(﹣ 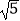 ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
(1)求椭圆E的方程;
(2)过坐标原点O的直线交椭圆W: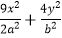 =1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB.
=1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
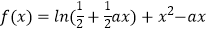 .(a为常数,a>0) (Ⅰ)若
.(a为常数,a>0) (Ⅰ)若 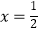 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;
(Ⅱ)求证:当0<a≤2时,f(x)在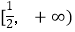 上是增函数;
上是增函数;
(Ⅲ)若对任意的a∈(1,2),总存在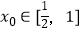 ,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣a|+a.
(1)若不等式f(x)≤6的解集为{x|﹣2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m﹣f(﹣n)成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】把函数f(x)=
 cos2x﹣sin2x的图象向右平移
cos2x﹣sin2x的图象向右平移  个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
A.[﹣ ,0]
,0]
B.[﹣π,0]
C.[﹣ ,
,  ]
]
D.[0, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】《张邱建算经》是中国古代数学史上的杰作,该书中有首古民谣记载了一数列问题:“南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸① , 头圈一尺三② . 逐节多三分③ , 逐圈少分三④ . 一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?”(注释:①第一节的高度为0.5尺;②第一圈的周长为1.3尺;③每节比其下面的一节多0.03尺;④每圈周长比其下面的一圈少0.013尺) 问:此民谣提出的问题的答案是( )
A.72.705尺
B.61.395尺
C.61.905尺
D.73.995尺
相关试题

