搜索
【题目】已知椭圆E： 
=1（a＞b＞0）的左焦点F1（﹣ 
，0），若椭圆上存在一点D，满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
（1）求椭圆E的方程；
（2）过坐标原点O的直线交椭圆W： 
=1于P、A两点，其中点P在第一象限，过P作x轴的垂线，垂足为C，连结AC并延长交椭圆W于B，求证：PA⊥PB．
参考答案：
【答案】
（1）
解：连接DF2，FO（O为原点，F2为右焦点），由题意知：椭圆的右焦点为 
，
因为FO是△DF1F2的中位线，且DF1⊥FO，所以|DF2|=2|FO|=2b，
所以|DF1|=2a﹣|DF2|=2a﹣2b，故 
，
在Rt△FOF1中， 
，
即b2+（a﹣b）2=c2=5，又b2+5=a2，解得a2=9，b2=4，
所以椭圆E的方程为 
（2）
解：由（Ⅰ）得椭圆W的方程为 
，
设P（m，n），则A（﹣m，﹣n），C（m，0），
∴ 
， 
，直线 
，
联立方程组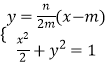 
，化简得 
，
∴ 
因为xA=﹣m，所以 
，则 
所以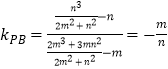 
，
则kPAkPB=﹣1，即PA⊥PB．
【解析】（I）用a，b，c表示出△OF1F的边长，利用勾股定理列方程解出a，b，即可；（II）设P（m，n），用m，n表示出直线AC的方程，求出B点坐标，计算PA，PB的斜率即可得出结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．
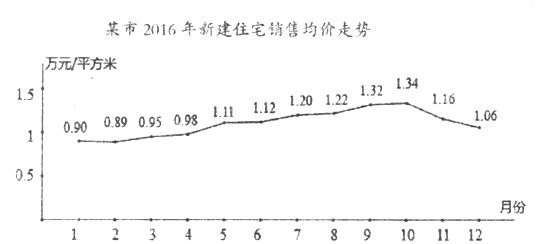
（Ⅰ）地产数据研究院研究发现，3月至7月的各月均价y（万元/平方米）与月份x之间具有较强的线性相关关系，试建立y关于x的回归方程（系数精确到0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；
（Ⅱ）地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．
参考数据：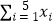
=25，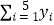 
=5.36， 
=0.64
回归方程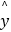
= 
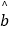x+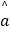 
中斜率和截距的最小二乘估计公式分别为： = 
， = 
﹣ 
． -
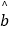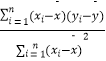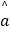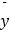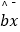科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，D1E⊥CD，AB=2BC=2．
（1）求证：BC⊥D1E；
（2）若平面BCC1B1与平面BED1所成的锐二面角的大小为
，求线段D1E的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于M，交AC于N．
（1）若∠ABC=70°，则∠MNA的度数是__．
（2）连接NB，若AB=8cm，△NBC的周长是14cm．
①求BC的长；
②在直线MN上是否存在P，使由P、B、C构成的△PBC的周长值最小？若存在，标出点P的位置并求△PBC的周长最小值；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
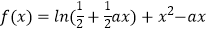．（a为常数，a＞0） （Ⅰ）若 
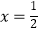是函数f（x）的一个极值点，求a的值；
（Ⅱ）求证：当0＜a≤2时，f（x）在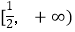
上是增函数；
（Ⅲ）若对任意的a∈（1，2），总存在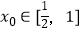
，使不等式f（x0）＞m（1﹣a2）成立，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l的极坐标方程为ρsin（θ+
）= 
，圆C的参数方程为： 
（其中θ为参数）．
（1）判断直线l与圆C的位置关系；
（2）若椭圆的参数方程为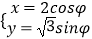
（φ为参数），过圆C的圆心且与直线l垂直的直线l′与椭圆相交于A，B两点，求|AB|． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=|2x﹣a|+a．
（1）若不等式f（x）≤6的解集为{x|﹣2≤x≤3}，求实数a的值；
（2）在（1）的条件下，若存在实数n使f（n）≤m﹣f（﹣n）成立，求实数m的取值范围．
相关试题
