【题目】一次函数 ![]() 与二次函数
与二次函数 ![]() 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
参考答案:
【答案】B
【解析】A.由一次函数的图象可知,a>0,b>0,由二次函数图象可知,a<0,b<0,故错误.
B.由一次函数的图象可知,a<0,b<0,由二次函数图象可知,a<0,b<0,正确;
C.由一次函数的图象可知,a>0,b>0,由二次函数图象可知,a>0,b<0,故错误.
D.由一次函数的图象可知,a<0,b>0,由二次函数的图象可知,a<0,b<0,故错误.
所以答案是:B.
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
问题发现:学完四边形的有关知识后,创新小组的同学进一步研究特殊的四边形,发现了一个结论.如图1,已知四边形
 是正方形,根据勾股定理和正方形的性质,很容易能够证明
是正方形,根据勾股定理和正方形的性质,很容易能够证明 .
.问题探究:
(1)如图2,已知四边形
 是矩形,若
是矩形,若 ,则
,则 的值是 ;
的值是 ; 的值是 ;
的值是 ;(2)如图3,已知四边形
 是菱形,证明:
是菱形,证明: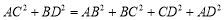 ;
;拓广探索:
(3)智慧小组看了创新小组交流后,提出了一个猜想,如图4,在
 中,
中,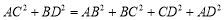 ,你认为这个猜想正确吗?请说明理由;
,你认为这个猜想正确吗?请说明理由;(4)请用文字语言叙述
 中得出的结论.
中得出的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )

A.55°
B.70°
C.125°
D.145° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面坐标系中,A(a,0),B(b,0),C(x,y)且满足(a+b)2+|a﹣b﹣4|=0,y=
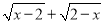 +2.
+2.(1)求三角形ABC的面积;
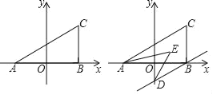
(2)若过B作BD∥AC交y轴于D,且AE、DE平分∠CAB、∠ODB,如图,求∠AED的度数;
(3)在y轴上是否存在点P,①使得△ABC和△ACP的面积相等,若存在,求出P点的坐标:若不存在,请说明理由;②若△ACP的面积是△ABC面积的2018倍成立,直接写出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
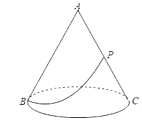
A.3m
B.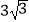 m
m
C.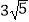 m
m
D.4m -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).

①将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
②将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
③直接写出点B2 , C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队在一次联赛中共进行了10场比赛,已知这10场比赛的平均得分为48分,且前9场比赛的得分依次为:57,51,45,51,44,46,45,42,48.
(1)求第10场比赛的得分;
(2)直接写出这10场比赛的中位数,众数和方差.
相关试题

