【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
①将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
②将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
③直接写出点B2 , C2的坐标.
参考答案:
【答案】解:如图,△A1B1C1 , △AB2C2即为所求
点B2(4,﹣2),C2(1,﹣3)
【解析】①利用点平移的规律写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
②利用网格特点和旋转的性质画出点B、C的对应点B2、C2 , 从而得到△AB2C2;
③再写出点B2、C2的坐标。
【考点精析】本题主要考查了平移的性质和旋转的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
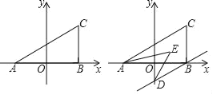
查看答案和解析>>【题目】如图,在平面坐标系中,A(a,0),B(b,0),C(x,y)且满足(a+b)2+|a﹣b﹣4|=0,y=
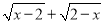 +2.
+2.(1)求三角形ABC的面积;
(2)若过B作BD∥AC交y轴于D,且AE、DE平分∠CAB、∠ODB,如图,求∠AED的度数;
(3)在y轴上是否存在点P,①使得△ABC和△ACP的面积相等,若存在,求出P点的坐标:若不存在,请说明理由;②若△ACP的面积是△ABC面积的2018倍成立,直接写出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
 与二次函数
与二次函数  在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
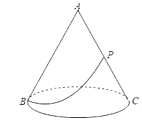
查看答案和解析>>【题目】如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m
B.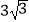 m
m
C.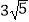 m
m
D.4m -
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队在一次联赛中共进行了10场比赛,已知这10场比赛的平均得分为48分,且前9场比赛的得分依次为:57,51,45,51,44,46,45,42,48.
(1)求第10场比赛的得分;
(2)直接写出这10场比赛的中位数,众数和方差.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组
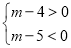 ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2
 =(1+
=(1+ )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把部分a+b 的式子化为平方式的方法。
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得a=________, b=___________.
)2,用含m、n的式子分别表示a、b,得a=________, b=___________.(2)若a+4
 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值。
)2,且a、m、n均为正整数,求a的值。
相关试题

