【题目】综合与实践:
问题发现:学完四边形的有关知识后,创新小组的同学进一步研究特殊的四边形,发现了一个结论.如图1,已知四边形![]() 是正方形,根据勾股定理和正方形的性质,很容易能够证明
是正方形,根据勾股定理和正方形的性质,很容易能够证明![]() .
.
问题探究:
(1)如图2,已知四边形![]() 是矩形,若
是矩形,若![]() ,则
,则![]() 的值是 ;
的值是 ;![]() 的值是 ;
的值是 ;
(2)如图3,已知四边形![]() 是菱形,证明:
是菱形,证明:![]() ;
;
拓广探索:
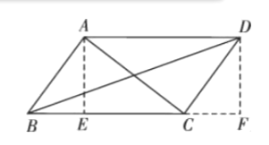
(3)智慧小组看了创新小组交流后,提出了一个猜想,如图4,在![]() 中,
中,![]() ,你认为这个猜想正确吗?请说明理由;
,你认为这个猜想正确吗?请说明理由;
(4)请用文字语言叙述![]() 中得出的结论.
中得出的结论.

参考答案:
【答案】(1)50,50;(2)见解析;(3)正确,理由见解析;(4)答案不唯一,例如:“平行四边形两对角线的平方和等于四条边的平方和”或“平行四边形的四条边的平方和等于两对角线的平方和”
【解析】
(1)根据矩形的性质可得:AB=CD=4,BC=AD=3,根据勾股定理可得![]() 、
、![]() ,继而求解;
,继而求解;
(2)根据菱形的性质可得:AC⊥BD,AB=BC=CD=AD,OA=OC,OB=OD,根据勾股定理即可求证;
(3)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,由四边形
,由四边形![]() 是平行四边形,求证Rt△ABE≌Rt△DCF,得出BE=CF,由勾股定理即可求出
是平行四边形,求证Rt△ABE≌Rt△DCF,得出BE=CF,由勾股定理即可求出
![]() ,
, ![]() ,继而求证;
,继而求证;
(4)根据题(3)求证结果即可解答.
解:(1) 在矩形ABCD中,AB=4,BC=3,∠ABC=∠BCD=∠ADC=∠BAD=90°
∴AB=CD=4,BC=AD=3,
在Rt△ABC中,由勾股定理可得:
![]()
在Rt△BCD中,由勾股定理可得:
![]()
∴![]()
∵BC=AD=3,
∴![]()
∴![]()
![]() 证明:
证明:![]() 四边形
四边形![]() 是菱形
是菱形
![]() ,AB=BC=CD=AD,OA=OC,OB=OD,
,AB=BC=CD=AD,OA=OC,OB=OD,
在![]() 中,由勾股定理,得
中,由勾股定理,得![]()
同理,可得![]()
![]()
![]()
![]()
![]()
![]()
![]() 这个结论正确
这个结论正确
理由如下:
如图,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() .
.
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
![]()
![]()
根据勾股定理,得
![]()
![]()
![]()
![]()
![]()
![]()
![]() 答案不唯一,例如:“平行四边形两对角线的平方和等于四条边的平方和”或“平行四边形的四条边的平方和等于两对角线的平方和”.
答案不唯一,例如:“平行四边形两对角线的平方和等于四条边的平方和”或“平行四边形的四条边的平方和等于两对角线的平方和”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+
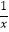 =3,则下列三个等式:①x2+
=3,则下列三个等式:①x2+ 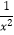 =7,②x﹣
=7,②x﹣ 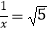 ,③2x2﹣6x=﹣2中,正确的个数有( )
,③2x2﹣6x=﹣2中,正确的个数有( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017
B.2016
C.191
D.190 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A.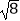 ﹣
﹣ 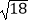 =﹣
=﹣ 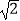
B.(﹣0.1)﹣2=0.01
C.(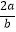 )2÷
)2÷ 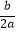 =
= 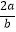
D.(﹣m)3?m2=﹣m6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )

A.55°
B.70°
C.125°
D.145° -
科目: 来源: 题型:
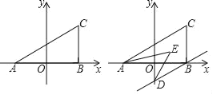
查看答案和解析>>【题目】如图,在平面坐标系中,A(a,0),B(b,0),C(x,y)且满足(a+b)2+|a﹣b﹣4|=0,y=
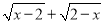 +2.
+2.(1)求三角形ABC的面积;
(2)若过B作BD∥AC交y轴于D,且AE、DE平分∠CAB、∠ODB,如图,求∠AED的度数;
(3)在y轴上是否存在点P,①使得△ABC和△ACP的面积相等,若存在,求出P点的坐标:若不存在,请说明理由;②若△ACP的面积是△ABC面积的2018倍成立,直接写出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
 与二次函数
与二次函数  在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
相关试题

