【题目】如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() =k.已知关于x,y的二元一次方程
=k.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
A.![]()
B.1
C.![]()
D.![]()
参考答案:
【答案】B
【解析】 ∵ 矩形A′B′C′D′与矩形ABCD是位似图形,![]() =k,顶点A的坐标为(1,t), ∴ 点A′的坐标为(k,kt),
=k,顶点A的坐标为(1,t), ∴ 点A′的坐标为(k,kt),
∵ 矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心, ∴ 矩形A′B′C′D′也关于点O成中心对称.
∵关于x,y的二元一次方程![]() (m,n是实数)无解,∴ mn=3,且n≠1,即n=
(m,n是实数)无解,∴ mn=3,且n≠1,即n=![]() (m≠3),
(m≠3),
∵以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,∴反比例函数n=![]() 的图象只经过点A′或C′,
的图象只经过点A′或C′,
∵矩形A′B′C′D′关于点O成中心对称,反比例函数n=![]() 的图象关于点O成中心对称,∴反比例函数n=
的图象关于点O成中心对称,∴反比例函数n=![]() 的图象经过C′点,
的图象经过C′点,
如果反比例函数n=![]() 的图象不经过C′点,则以m,n为坐标(记为(m,n)的所有的点中,如果有点落在矩形A′B′C′D′的边上,
的图象不经过C′点,则以m,n为坐标(记为(m,n)的所有的点中,如果有点落在矩形A′B′C′D′的边上,
则至少有两个点落在矩形A′B′C′D′的边上,∴A′点的坐标是(3,1),∴kt=1.故答案选:B
首先求出点A′的坐标为(k,kt),再根据关于x,y的二元一次方程![]() (m,n是实数)无解,可得mn=3,且n≠1;然后根据以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,可得反比例函数n=
(m,n是实数)无解,可得mn=3,且n≠1;然后根据以m,n为坐标(记为(m,n)的所有的点中,有且只有一个点落在矩形A′B′C′D′的边上,可得反比例函数n=![]() 的图象只经过点A′或C′;最后判断出反比例函数n=
的图象只经过点A′或C′;最后判断出反比例函数n=![]() 的图象经过C′点,则A′点的坐标是(3,1),所以kt=1,据此解答即可.
的图象经过C′点,则A′点的坐标是(3,1),所以kt=1,据此解答即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);
(2)根据(1)中所画图象,完成下列表格:两人相遇次数
(单位:次)1
2
3
4
…
n
两人所跑路程之和
(单位:m)100
300
…
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.

(1)函数y=ax2-2ax+a+3(a>0)的最小值为 , 当二次函数L1 , L2的y值同时随着x的增大而减小时,x的取值范围是
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程-a(x+1)2+1=0的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.

(1)特例探索
如图1,当∠ABE=45°,c=2 时,a= ,b= .
时,a= ,b= .
如图2,当∠ABE=30°,c=4时,a= ,b= .
(2)归纳证明
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)如图4,在ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ,AB=3,求AF的长.
,AB=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则ABCD的面积等于

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=
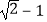 ,则∠ACD= .
,则∠ACD= .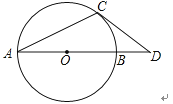
-
科目: 来源: 题型:
查看答案和解析>>【题目】写一个你喜欢的实数m的值 ,使得事件“对于二次函数
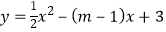 ,当x<﹣3时,y随x的增大而减小”成为随机事件.
,当x<﹣3时,y随x的增大而减小”成为随机事件.
相关试题

