Question

【题目】如图，已知二次函数L1：y=ax2-2ax+a+3（a＞0）和二次函数L2：y=-a（x+1）2+1（a＞0）图象的顶点分别为M，N，与y轴分别交于点E，F．

（1）函数y=ax2-2ax+a+3（a＞0）的最小值为　 ， 当二次函数L1 ， L2的y值同时随着x的增大而减小时，x的取值范围是
（2）当EF=MN时，求a的值，并判断四边形ENFM的形状（直接写出，不必证明）．
（3）若二次函数L2的图象与x轴的右交点为A（m，0），当△AMN为等腰三角形时，求方程-a（x+1）2+1=0的解．

Answer 1

【答案】
（1）3；﹣1≤x≤1
（2）

解：由二次函数L1：y=ax2-2ax+a+3可知E（0，a+3），

由二次函数L2：y=-a（x+1）2+1=﹣a2x-2ax-a+1可知F（0，-a+1），

∵M（1，3），N（-1，1），

∴EF=MN==2，

∴a+3-（-a+1）=2，

∴a=-1，

作MG⊥y轴于G，则MG=1，作NH⊥y轴于H，则NH=1，

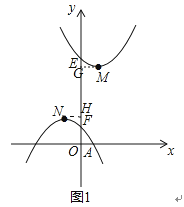
∴MG=NH=1，

∵EG=a+3-3=a，FH=1-（-a+1）=a，

∴EG=FH，

在△EMG和△FNH中，

，

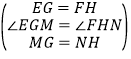∴△EMG≌△FNH（SAS），

∴∠MEF=∠NFE，EM=NF，

∴EM∥NF，

∴四边形ENFM是平行四边形；

∵EF=MN，

∴四边形ENFM是矩形

（3）

解：由△AMN为等腰三角形，可分为如下三种情况：

①如图2，

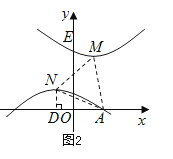
当MN=NA=2时，过点N作ND⊥x周，垂足为点D，则有ND=1，DA=m-（-1）=m+1，

在Rt△NDA中，NA2=DA2+ND2，即（2）2=（m+1）2+12，

∴m1=-1，m2=--1（不合题意，舍去），

∴A（-1，0）．

由抛物线y=-a（x+1）2+1（a＞0）的对称轴为x=-1，

∴它与x轴的另一个交点坐标为（-1-，0）．

∴方程-a（x+1）2+1=0的解为x1=﹣1，x2=-1-．

②如图3，

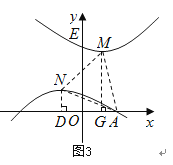
当MA=NA时，过点M作MG⊥x轴，垂足为G，则有OG=1，MG=3，GA=|m-1|，

∴在Rt△MGA中，MA2=MG2+GA2，即MA2=32+（m-1）2，

又∵NA2=（m+1）2+12，

∴（m+1）2+12=32+（m-1）2，m=2，

∴A（2，0），

则抛物线y=-a（x+1）2+1（a＞0）的左交点坐标为（-4，0），

∴方程-a（x+1）2+1=0的解为x1=2，x2=-4．

③当MN=MA时，32+（m-1）2=（2）2，

∴m无实数解，舍去．

综上所述，当△AMN为等腰三角形时，方程-a（x+1）2=0的解为

x1=-1，x2=-1-或x1=2，x2=-4．

【解析】（1）把二次函数L1：y=ax2-2ax+a+3化成顶点式，即可求得最小值，分别求得二次函数L1 ， L2的y值随着x的增大而减小的x的取值，从而求得二次函数L1 ， L2的y值同时随着x的增大而减小时，x的取值范围；
（2）先求得E、F点的坐标，作MG⊥y轴于G，则MG=1，作NH⊥y轴于H，则NH=1，从而求得MG=NH=1，然后证得△EMG≌△FNH，∠MEF=∠NFE，EM=NF，进而证得EM∥NF，从而得出四边形ENFM是平行四边形；
（3）作MN的垂直平分线，交MN于D，交x轴于A，先求得D的坐标，继而求得MN的解析式，进而就可求得直线AD的解析式，令y=0，求得A的坐标，根据对称轴从而求得另一个交点的坐标，就可求得方程-a（x+1）2+1=0的解．
此题考查了二次函数的综合应用，包括函数表达式，增减性问题，平行四边形判定，相似三角形等.