【题目】我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.
(1)特例探索
如图1,当∠ABE=45°,c=2![]() 时,a= ,b= .
时,a= ,b= .
如图2,当∠ABE=30°,c=4时,a= ,b= .
(2)归纳证明
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)如图4,在ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
参考答案:
【答案】
(1)2![]() ;2
;2![]() ;2
;2![]() ;2
;2![]()
(2)
解:猜想:a2+b2=5c2,
如图3,连接EF,

设∠ABP=α,
∴AP=csinα,PB=ccosα,
由(1)同理可得,PF=![]() PA=
PA=![]() ,PE=
,PE=![]() PB=
PB=![]() ,
,
AE2=AP2+PE2=c2sin2α+![]() ,BF2=PB2+PF2=
,BF2=PB2+PF2=![]() +c2cos2α,
+c2cos2α,
∴![]() =c2sin2α+
=c2sin2α+![]() ,
,![]() =
=![]() +c2cos2α,
+c2cos2α,
∴![]() +
+![]() =
=![]() +c2cos2α+c2sin2α+
+c2cos2α+c2sin2α+![]() ,
,
∴a2+b2=5c2;
(3)
解:如图4,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,

∵点E、G分别是AD,CD的中点,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=2![]() ,
,
∴∠EAH=∠FCH,
∵E,F分别是AD,BC的中点,
∴AE=![]() AD,BF=
AD,BF=![]() BC,
BC,
∴AE=BF=CF=![]() AD=
AD=![]() ,
,
∵AE∥BF,
∴四边形ABFE是平行四边形,
∴EF=AB=3,AP=PF,
在△AEH和△CFH中,
 ,
,
∴△AEH≌△CFH,
∴EH=FH,
∴EQ,AH分别是△AFE的中线,
由(2)的结论得:AF2+EF2=5AE2,
∴AF2=5![]() ﹣EF2=16,
﹣EF2=16,
∴AF=4.
【解析】(1)由等腰直角三角形的性质得到AP=BP=![]() AB=2,根据三角形中位线的性质,得到EF∥AB,EF=
AB=2,根据三角形中位线的性质,得到EF∥AB,EF=![]() AB=
AB=![]() ,再由勾股定理得到结果;
,再由勾股定理得到结果;
(2)连接EF,设∠ABP=α,类比着(1)即可证得结论.
(3)连接AC交EF于H,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,AD=BC=2![]() ,∠EAH=∠FCH根据E,F分别是AD,BC的中点,得到AE=BF=CF=
,∠EAH=∠FCH根据E,F分别是AD,BC的中点,得到AE=BF=CF=![]() AD=
AD=![]() ,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由(2)的结论得即可得到结果.
,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由(2)的结论得即可得到结果.
【考点精析】通过灵活运用相似三角形的应用,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=ax+b与双曲线y=
 (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);
(2)根据(1)中所画图象,完成下列表格:两人相遇次数
(单位:次)1
2
3
4
…
n
两人所跑路程之和
(单位:m)100
300
…
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数L1:y=ax2-2ax+a+3(a>0)和二次函数L2:y=-a(x+1)2+1(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.

(1)函数y=ax2-2ax+a+3(a>0)的最小值为 , 当二次函数L1 , L2的y值同时随着x的增大而减小时,x的取值范围是
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程-a(x+1)2+1=0的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,
 =k.已知关于x,y的二元一次方程
=k.已知关于x,y的二元一次方程 (m,n是实数)无解,在以m,n为坐标记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
A.
B.1
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则ABCD的面积等于

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=
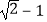 ,则∠ACD= .
,则∠ACD= .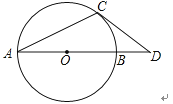
相关试题

