【题目】如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=![]() ,则∠ACD= .
,则∠ACD= .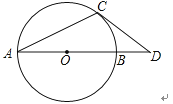
参考答案:
【答案】112.5°
【解析】解:如图,连结OC.
∵DC是⊙O的切线,
∴OC⊥DC,
∵BD=![]() ﹣1,OA=OB=OC=1,
﹣1,OA=OB=OC=1,
∴OD=![]() ,
,
∴CD=![]() =
=![]() =1,
=1,
∴OC=CD,
∴∠DOC=45°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=![]() ∠DOC=22.5°,
∠DOC=22.5°,
∴∠ACD=∠OCA+∠OCD=22.5°+90°=112.5°.
所以答案是:112.5.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“称为中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均称为“中垂三角形”,设BC=a,AC=b,AB=c.

(1)特例探索
如图1,当∠ABE=45°,c=2 时,a= ,b= .
时,a= ,b= .
如图2,当∠ABE=30°,c=4时,a= ,b= .
(2)归纳证明
请你观察(1)中的计算结果,猜想a2 , b2 , c2三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)如图4,在ABCD中,点E、F、G分别是AD,BC,CD的中点,BE⊥EG,AD=2 ,AB=3,求AF的长.
,AB=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,
 =k.已知关于x,y的二元一次方程
=k.已知关于x,y的二元一次方程 (m,n是实数)无解,在以m,n为坐标记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
A.
B.1
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,E为AD的中点,BE,CD的延长线相交于点F,若△DEF的面积为1,则ABCD的面积等于

-
科目: 来源: 题型:
查看答案和解析>>【题目】写一个你喜欢的实数m的值 ,使得事件“对于二次函数
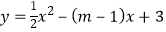 ,当x<﹣3时,y随x的增大而减小”成为随机事件.
,当x<﹣3时,y随x的增大而减小”成为随机事件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1 , 连接AC1 , BD1 . 如果四边形ABD1C1是矩形,那么平移的距离为 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
 ﹣(
﹣( ﹣π)0﹣2
﹣π)0﹣2 sin60°
sin60°
(2)化简:(1+ )
) .
.
相关试题

